原文地址:https://cos.name/2016/11/conjugate-gradient-for-regression/
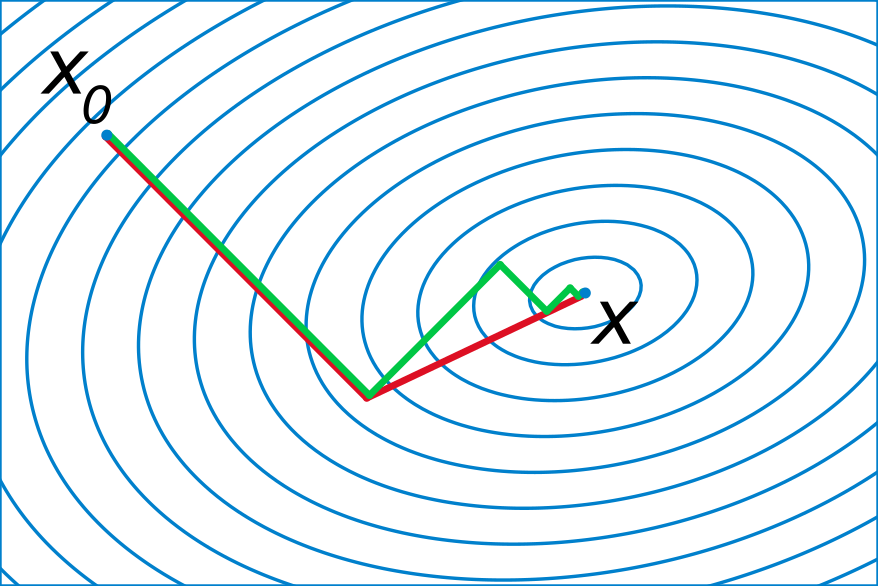
共轭梯度示意图(图片来源:维基百科)
轮回眼 共轭梯度示意图(图片来源:维基百科)
引子
之所以写这篇文章,是因为前几天统计之都的微信群里有同学提了一个问题,想要对一个很大的数据集做回归。然后大家纷纷给出了自己的建议,而我觉得共轭梯度算回归的方法跟这个背景比较契合,所以就正好写成一篇小文,与大家分享一下。
说到算回归,或许大家都会觉得这个问题太过简单了,如果用 \(X\) 表示自变量矩阵,\(y\) 表示因变量向量,那么回归系数的最小二乘解就是 \(\hat{\beta}=(X'X)^{-1}X'y\)。(本文完)
哎等等,别真走啊,我们的主角共轭梯度还没出场呢。前面的这个算系数的公式确实非常简洁、优雅、纯天然、不做作,但要往里面深究的话,还是有很多问题值得挖掘的。
最简单暴力的方法,就是从左向右,依次计算矩阵乘法,矩阵求逆,又一个矩阵乘法,最后是矩阵和向量的乘法。如果你就是这么算的,那么可以先默默地去面壁两分钟了。
更合理的方法,要么是对 \(X'X\) 进行 Cholesky 分解,要么是对 \(X\) 进行 QR 分解,它们基本上是现在算回归的软件中最常见的方法。关于暴力方法和矩阵分解方法的介绍和对比,可以参见这个B站上的视频。(什么?你问我这么严肃的话题为什么要放B站上?因为大部分时间都是在吐槽啊)
好,刚才去面壁的同学现在应该已经回来了,我们继续。前面这些通过矩阵运算求回归系数的方法,我们可以统称为直接法。叫这个名字,是因为它们都可以在确定数目的步骤内得到最终的结果。而与之相对的,则叫做迭代法,意思是通过不断更新已经得到的结果,来逐渐逼近真实的取值。打个比方,你想要知道一瓶82年的拉菲值多少钱,直接法就是去做调研,原料值多少,品牌值多少,加工费多少,运输费多少……然后加总起来得到最终的定价;而迭代法就是去问酒庄老板,你先随便蒙一个数,然后老板告诉你高了还是低了,反复循环,总能猜个八九不离十。
说到这里,你自然要问了,既然算回归的软件大都是用直接法,为什么还要考虑迭代法?莫非直接法有什么不好的地方?这就说到问题的点子上了。
首先,如果我们假设数据有 \(n\) 行 \(p\) 列,那么我们会发现,\(X'X\) 的维度就是 \(p\times p\),而如果变量数特别多,那么这个矩阵就会以平方的速度增大,那时候不要说算矩阵分解,即使是要存储这个大矩阵,可能都会遇到很多麻烦。
第二点,往好的方面讲,直接法给出的结果精度一般非常高,但在许多实际问题中,可能小数点后面三位保证正确就足够了,而直接法可能会为了保证十三位的精度而多出非常多的计算量。用直接法得到高精度的结果,再舍入成低精度的实际需求,总有一种买椟还珠的感觉。相反,迭代法是一个向真相逐渐靠近的过程,如果在中途已经可以保证需要的精度,那么就随时可以停止,节省计算时间。
第三点就更偏技术层面一点。通常而言,如果数据很大,那么很有可能矩阵 \(X\) 会带有某种稀疏特性,也就是说其中会有非常多的零元素。稀疏矩阵具有一些高效的存储方法和矩阵运算算法,但用直接法得到 \(X'X\) 之后,它就往往不再是稀疏矩阵了,于是存储量和计算量都会陡增。换言之,本来具有计算优势的稀疏矩阵,在直接法中却并不能发挥出它的优势来。
那么是不是有某种迭代法可以克服这些缺点呢?巧的是,本文要介绍的共轭梯度法就是其中之一。(哎说实话写这句的时候我自己都不信有多巧,前面铺垫这么多+设问句+巧合明显是作者刻意安排的啊,太明显了……)
什么是共轭梯度法?
共轭,其实是线性代数里面的一个概念。给定一个正定矩阵 \(A\),如果两个向量 \(u\) 和 \(v\) 满足 \(u'Av=0\),就说 \(u\) 和 \(v\) 是关于 \(A\) 共轭的。一个 \(m\times m\) 的正定矩阵,最多可以有 \(m\) 组相互共轭的向量,而它们就组成了 \(m\) 维向量空间里的一组基 \(\{p_1,p_2,\ldots,p_m\}\)。通过线性代数的知识我们知道,给定了一组基后,向量空间里的任何一个元素就可以写成这组基的线性组合,比如
\[x=\sum_{i=1}^m \alpha_i p_i.\]
在回归模型中,回归系数 \(\hat{\beta}\) 正是线性方程组 \(Ax=b\) 的解,其中 \(A=X'X\),\(b=X'y\)。而共轭梯度法(Conjugate gradient, CG),就是想像上面这个式子一样,把解 \(x\) 表达成共轭向量基的线性组合:只要依次算出所有的共轭向量 \(p_i\) 和对应的系数 \(\alpha_i\),就可以得出 \(x\)。而在实际情况中,有可能用更少数目的 \(p_i\) 就能得到对 \(x\) 的良好近似,于是在这个意义上 CG 就是一种迭代法了。
那么为什么要叫共轭“梯度”呢?这是因为前面的这个公式还有另一种理解。考虑一个函数 \(f(x)=\frac{1}{2}x'Ax-b'x\),我们很容易发现它取最小值的点正是方程 \(Ax=b\) 的解。如果我们用最优化的思路去解 \(Ax=b\),就是要找到一个 \(x\) 使得 \(f(x)\) 达到最小。一般情况下,我们会采用“最速下降”的算法,即给定一个初始值 \(x_0\),计算当前的梯度,然后沿着该梯度方向移动到下一个更新值 \(x_1\),再计算梯度,如此反复循环。而共轭梯度法,则是说我们并不是沿着梯度走,而是沿着所谓的“共轭梯度”,即 \(p_i\),进行移动。
至于为什么应该用共轭梯度而不是梯度,我建议感兴趣的读者看一看文章最后的那篇参考文献,其中对共轭梯度的优势进行了非常详细的阐述。一个直观的理解就是,普通的梯度法往往会有重复移动的方向(如文首图片中的绿线),而共轭梯度保证了每次移动的方向是共轭的(即关于 \(A\) 是正交的,如文首图片中的红线),因此不会有重复的劳动。关于 CG 的理论说来那个话就长了,因此本文不在这方面做过多的论述(其实是因为作者太懒),我在这里更想强调的其实是它的计算过程,参见图 1。

图1:共轭梯度法算法流程
神奇在哪里?
图 1 所示的算法基本上可以展现出 CG 最重要的几个特性。
首先第一点,从图 1 可以看出,与 \(A\) 有关的运算只是一个矩阵乘法 \(Ap_k\),剩下的部分都是向量之间的运算,没有任何其他更复杂的操作。而我们知道,矩阵与向量的乘法是很容易编程实现的,而且即使当矩阵很大的时候,它的内存占用量也非常小。纵观整个算法,基本上只需要存储若干个向量,所以在这个层面上,共轭梯度法非常适合内存受限的情形。
然后第二点,就如之前所说,共轭梯度法是一种迭代法,但它最奇特的一点在于,它同时又能保证在 \(m\) 步内完成计算。所以从某种层面上说,它兼具了直接法和迭代法的优点,好的情形下可以提前终止,最差的情况也能在 \(m\) 步内完成。
第三点,由于共轭梯度法中的大矩阵只参与乘法运算,所以稀疏矩阵的高效算法就可以派上用场了。可能你会说,\(A=X'X\) 不是已经破坏了稀疏性了吗?但实际上,在计算 \(Ap_k\) 的时候,可以先计算 \(v=Xp_k\),再计算 \(Ap_k=X'v\),这样两步分开来都是稀疏矩阵的运算。
代码实现
如前所说,CG 的一大优势在于编程实现非常简单。不依赖于任何附加包,我们就可以用几十行 R 代码搞定其核心算法。
## Target: solve linear equation Ax = b. A is positive definite
## Ax -- A function to calculate the matrix-vector product
## `A * x` given a vector `x` as the first argument
## b -- Vector of the right hand side of the equation
## x0 -- Initial guess of the solution
## eps -- Precision parameter
## verbose -- Whether to print out iteration information
cg = function(Ax, b, x0 = rep(0, length(b)), eps = 1e-6,
verbose = TRUE, ...)
{
m = length(b)
x = x0
r = b - Ax(x0, ...)
p = r
r2 = sum(r^2)
for(i in 1:m)
{
Ap = Ax(p, ...)
alpha = r2 / sum(p * Ap)
x = x + alpha * p
r = r - alpha * Ap
r2_new = sum(r^2)
err = sqrt(r2_new)
if(verbose)
cat(sprintf("Iteration %d, err = %.8f\n", i, err))
if(err < eps)
break
beta = r2_new / r2
p = r + beta * p
r2 = r2_new
}
x
}或许会有读者疑问,为什么我要把矩阵乘法定义成一个函数参数 Ax,而不是直接在算法过程中写矩阵乘法。这是因为,某些情况下矩阵乘法可能有特殊的实现,用户只需要定义好相应的函数,就可以直接调用上面的这段程序,而不需要去修改算法的细节。使用上面的程序,一个简单的模拟例子如下:
## Simulation example
set.seed(123)
n = 10000
p = 1000
x = matrix(rnorm(n * p), n)
b = rnorm(p)
y = x %*% b
beta_direct = solve(crossprod(x), crossprod(x, y))
mat_vec_mult = function(x, mat)
{
as.numeric(crossprod(mat, mat %*% x))
}
xy = as.numeric(crossprod(x, y))
beta_cg = cg(mat_vec_mult, xy, mat = x)
max(abs(beta_direct - beta_cg))
## [1] 7.422063e-12其中 CG 程序打印出了如下的信息:
Iteration 1, err = 80261.88521243
Iteration 2, err = 24276.83688338
...
Iteration 21, err = 0.00000622
Iteration 22, err = 0.00000197
Iteration 23, err = 0.00000062可以看出,CG 在第 23 步迭代后就收敛了,在我的机器上耗时约 0.82 秒,而直接法总共耗时约 5.3 秒,是 CG 的将近 6.5 倍。
真有这么神奇?
看到这个结果,我估计小伙伴们都惊呆了。如果效果真这么好,那赶紧拿它去跑跑回归试试啊。于是我到 UCI 机器学习数据库上找了一个中等大小的数据集,包含 53500 个观测和 384 个自变量,然后兴冲冲地跑了个 CG(这里完全只是为了演示算法,实际处理数据时,请千万千万先对数据的背景有所了解,然后再考虑建模,切记切记):
dat = read.csv("slice_localization_data.csv")
n = nrow(dat)
y = dat$reference
x = as.matrix(dat[, -c(1, ncol(dat))]) / sqrt(n)
xy = as.numeric(crossprod(x, y))
coeffs = cg(mat_vec_mult, xy, mat = x)
## Iteration 1, err = 11262.97730747
## Iteration 2, err = 4471.54099614
## Iteration 3, err = 1783.28640925
## ...
## Iteration 100, err = 2.94723420
## Iteration 101, err = 4.60232106
## Iteration 102, err = 4.02014578
## ...
## Iteration 200, err = 0.63018214
## Iteration 201, err = 1.67568741
## Iteration 202, err = 0.49243538
## ...
## Iteration 382, err = 0.16954617
## Iteration 383, err = 1.05050962
## Iteration 384, err = 0.11322079纳尼??怎么跟剧本写的不一样啊?说好的提前收敛呢?就算不提前不是说最多 \(m\) 步就收敛吗?我文章都写到这里了突然被打脸还怎么圆场啊?
(此处过去了半个小时……)
当崩塌的三观逐渐恢复的时候,就开始回过头来反思哪儿出了问题。其实,本文在之前有个非常重要的细节非常容易被忽视掉,大家把文章翻回第二节的第一句话,那里对矩阵 \(A\) 加了一个定语:正定。正定的代数意义表现在矩阵所有的特征值都大于 0,而在回归中,它等价于数据矩阵 \(X\) 是满秩的,换言之,没有多重共线性的存在。而如果我们检查一下这个数据中 \(X'X\) 的行列式,就会发现它等于 0,也就是说有多重共线性的存在——原来我们之前兴冲冲地犯了一个美丽的错误。
知道哪儿出错了就好办了,对于多重共线性,其中的一种应对办法就是给 \(X'X\) 的对角线上加上一个很小的常数 \(\lambda\),这也就是我们常说的岭回归。我们重新修改一个岭回归版的矩阵运算函数,设定好 \(\lambda\) 参数和精度,再放到 CG 中去运行:
ridge = function(x, mat, lambda = 0.01)
{
as.numeric(crossprod(mat, mat %*% x)) + lambda * x
}
coeffs_ridge = cg(ridge, xy, eps = 1e-3, mat = x, lambda = 0.01)
## Iteration 1, err = 11256.55983300
## Iteration 2, err = 4455.13459864
## Iteration 3, err = 1767.78523995
## ...
## Iteration 61, err = 0.00164239
## Iteration 62, err = 0.00127173
## Iteration 63, err = 0.00092021这一回迭代 63 次就以 0.001 的精度收敛了,耗时约 4.2 秒。而更进一步,如果查看原始数据就会发现,这个数据的稀疏比例非常大,所以我们可以把矩阵转换成稀疏格式,再来尝试运行 CG:
library(Matrix)
xsp = as(x, "sparseMatrix")
coeffs_sparse_ridge = cg(ridge, xy, eps = 1e-3, mat = xsp, lambda = 0.01)最后耗时约 2.6 秒。
总结
前面那个错误使用 CG 的例子并不是我杜撰的,而是我在准备这篇文章的时候真实发生的事情。对于我自己而言也是一个教训:跑算法跑模型的时候,一定要仔细检查假定条件,然后对数据要有充分的了解,否则前方的终点就会跟非正定的 CG 一样,不收敛啊。
相信通过模拟和实际数据的例子,读者可以更直观地感受到 CG 的如下一些优点:
- 实现简单,会矩阵乘法就行,不会的话请会的人吃顿饭就够了;
- 内存占用小,妈妈再也不用担心花钱给我加内存了;
- 可以控制收敛精度,想到哪儿停就到哪儿停;
- 可以充分利用稀疏矩阵或者其他特殊的矩阵构造加快运算,激发小宇宙潜能。
本文的代码可以在 Github 上查看和下载。
参考文献:An Introduction to the Conjugate Gradient Method without the Agonizing Plain
HarryZhu:对于非正定的矩阵,添加一个 lambda 参数 相当于增加了松弛变量,利用约束条件来填满多重共线性,不知道这样理解有没有问题1。
liyun:
- 基于各种下降迭代的解析解不仅仅适用于普通最小二乘,各种广义线性模型都可用,比如
logit;- 共轭梯度法还可以并行计算,这对本身就分布存储的非常大的数据(比如上亿行)就非常关键了。如果一定要用 QR分解,分布式的情况下就只能做 bootstrap 类了…。
个人觉得是加了以后对角线上的数就可以保证不再是 0,这样就可以避免多重共线性。↩