原文地址:https://zhuanlan.zhihu.com/p/19793523
双重差分吗,就是差分两次。我们先来举个栗子。
现在要修一条铁路,铁路是条线,所以必然会有穿过的城市和没有被穿过的城市。记\(D_i=1\),如果城市\(i\)被穿过,\(D_i=0\)如果城市\(i\)没有被穿过。
现在我们比较好奇铁路修好以后,被铁路穿过的城市是不是经济增长更快了?我们该怎么做呢?
一开始的想法是,我们把\(D_i=1\)的城市的 GDP 加总,减去\(D_i=0\)的城市的 GDP 加总,然后两者一减,即\(\mathrm{E}(Y_i|D_i==1)-\mathrm{E}(Y_i|D_i==0)\),这样我们就算出了两类城市的 GDP 的平均之差。
这样做不用说肯定有问题。万一被铁路穿过的城市在建铁路之前 GDP 就高呢?为了解决这个问题,我们需要观察到至少两期,第一期是建铁路之前,第二期是建铁路之后。我们先把两类城市的 GDP 做两期之差,即:
\[\Delta Y_i=\frac{1}{N}\sum(Y_{i1}-Y_{i0})\]
这是第一次差分,经过这一步,我们实际上算出了每个城市 GDP 的增长(率,如果取 log 之后),也就是 GDP 的趋势。
完了之后,计算:
\[\mathrm{Treatment Effect}=\mathrm{E}(\Delta Y_i|D_i=1)-\mathrm{E}(\Delta Y_i|D_i=0)\]
这是第二次差分。这一步就把两类城市在修建铁路之前和之后的 GDP 增长率的差异给算出来了,这就是我们要的处理效应,即修建铁路之后对城市经济的促进作用。
这个东西你还可以换一个写法。记\(T=1\)如果时间为建铁路之后,\(T=0\)如果时间为建铁路之前,那么我们可以得到一个表:
| Treated | \(D_i=0\) | \(D_i=1\) |
|---|---|---|
| \(T=0\) | 0 | 0 |
| \(T=1\) | 0 | 1 |
\(Treated\)代表在某一期,某一类城市是不是建了铁路。第零期肯定没有建铁路,第一期只有\(D_i=1\)的城市建了铁路。所以\(Treated=D_i*T\)。因此我们把方程写成:
\[Y_{it}=\alpha D_i+\beta T+\gamma(D_i\times T)+u_{it}\]
对时间差分,得到:
\[\Delta Y_i=\beta+\gamma D_i+\Delta u_{it}\]
再次差分,取期望:
\[\mathrm{E}(\Delta Y_1-\Delta Y_0)=\gamma\]
可见,\(\gamma\)就是我们想要估计的处理效应。
所以实际做的时候,可以直接跑
\[Y_{it}=\alpha D_i+\beta T+\gamma(D_i\times T)+u_{it}\]
这个式子的回归,得到的交叉项的系数就是所要估计的处理效应。
用一个图表示就是:
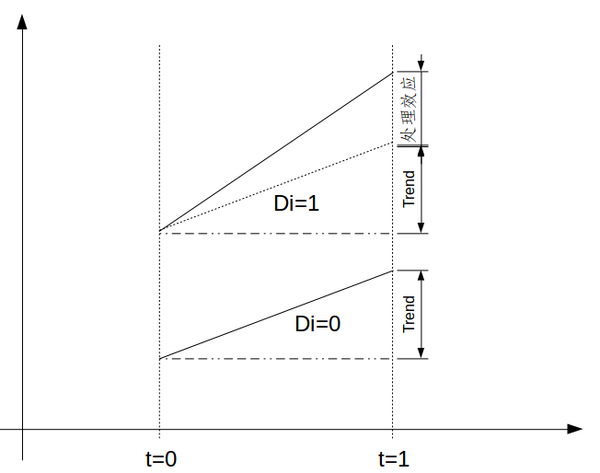
所以看清楚了,这里 DID 最关键的假设是 common trend,也就是两个组别在不处理的情况下,\(y\)的趋势是一样的。
那么你会说了,铁路穿过的城市可能本身 GDP 也高,而 GDP 高的城市按照理论 GDP 增长率可能更高可能更低,所以 common trend 的假设可能是不对的,那怎么办?
如果这个问题存在,我们可以进一步假设在控制了某些外生变量之后,common trend 是对的,比如上个问题,我们可以控制城市在\(T=0\)期的 GDP level。当我们控制其他变量之后,自然不能直接减两次了,我们需要用上面说的回归式子,即 run the following OLS:
\[Y_{it}=\alpha D_i+\beta T+\gamma(D_i\times T)+\boldsymbol{X}^\prime\delta+u_{it}\]
好了,我就说到这里了。当然也有可能你控制了\(X\)之后 common trend 还是不成立,那么你要想其他办法了。有些人会去找工具变量,这个方法我不是多么认可,所以我也就不介绍了。需要的时候再说。