原文地址:https://zhuanlan.zhihu.com/p/19862463
随着对社交网络(social network)研究的不断深入,一个现实的问题一直困扰着政策制定者和社交网络中的个人:可不可以识别出哪些人在一个社交网络中对信息传播有最强的影响力?或者说,社交网络中的个人究竟会不会知道社交网络中谁是影响力最大的?
这里的困难在于,无论对于政策制定者和社交网络中的个人,都不可能有完整的社交网络的信息(即谁是谁的朋友)。即使是身处社交网络中的个人,也只可能知道自己认识的人的信息,而对于自己的朋友之外的信息仍然很难获取。
之前的研究定义了社交网络中每个个体的“重要性”,或者说“集中度(centrality)”,比如特征向量集中度( eigenvector centrality )以及 Katz-Bonacich 集中度。但是这些定义前提是我们必须知道整个社交网络的信息。
Banerjee, Chandrasekhar, Duflo 以及 Jackson 等人在 NBER 上的一篇 working paper:GOSSIP: IDENTIFYING CENTRAL INDIVIDUALS IN A SOCIAL NETWORK从理论上解决了这一问题。这篇文章从理论上证明了,社交网络中的每个个体,通过简单的数一下每条消息传过来的源头的次数,个体可以知道社交网络中每个人的重要性(集中度)的排序。
故事是怎样的呢?假设一个社交网络中有\(n\)个个体,\(n\)个个体之间的关系可以通过一个矩阵\(g\)来表示(\(g_{i,j}=1\)表示\(i\)认识\(j\)),假设每个个体在得知一个消息(gossip)之后以\(p\)的概率告知其朋友,那么可以定义矩阵
\[\boldsymbol{\mathrm{H}}(\boldsymbol{g};p,T):=\sum^T_{t=1}(p\boldsymbol{g})^t\]
其中\(\boldsymbol{H}\)的第\(i,j\)个元素代表在消息传递了\(T\)次之后,第\(j\)个人从\(i\)得到消息的次数的期望。这样就可以定义一个传播的集中度(diffusion centrality):
\[\mathrm{DC}(\boldsymbol{g};p,T):=\boldsymbol{\mathrm{H}}(\boldsymbol{g};p,T)\cdot\boldsymbol{1}=\left(\sum^T_{t=1}(p\boldsymbol{g})^t\right)\cdot\boldsymbol{1}\]
这个集中度(以下简称 DC)代表了在经过了\(T\)次传播之后,第\(i\)个个体所传播的人数的期望值,这个个体能直接或者间接传播的人数越多,那么显然这个个体在社交网络中就越重要。其他的集中度定义(特征向量集中度、KB 集中度)在这里不赘述。
作者考虑了这么一个消息传播的过程(Gossip Process):有一个新消息(无论是消息是事实、猜测或者甚至是谣言、观点)从\(i\)传出,\(i\)可以告诉\(k\)和\(q\),\(k\)可能告诉\(j\),\(j\)可能告诉\(q\)和\(r\),但是在每一次传递中,每个人都告诉传递的下家,这条消息是从\(i\)这里传出来的。比如在这里,\(k\)从\(i\)这里听到了一次,而\(q\)则直接从\(i\)听到了一次,间接从\(j\)这里听到了一次,所以共两次。这里的关键点在于,这个过程并不需要每个人知道消息传播的路径,而仅仅需要知道消息是从谁传出来的,以及自己听到了多少次这个消息。这个计数过程可以如下描述:
\[\mathrm{NG}(\boldsymbol{g};p,T)_j:=\boldsymbol{\mathrm{H}}(\boldsymbol{g};p,T)_{\cdot j}\]
也就是\(\boldsymbol{\mathrm{H}}\)矩阵的第\(j\)列,代表了经过\(T\)次消息传递之后,\(j\)从每个个体听到消息的期望次数。
作者证明了,每个人的排序与定义的\(\mathrm{DC}\)是正相关的,而且随着\(T\)趋向于无穷,每个个体都可以完美的知道每个人的集中度的排序。
好了,证明了上面的结论,你能拿出点证据来说明你的理论是对的么?
作者于是需要证明,每个个体的确有识别出“八卦之王”的能力。
于是,作者调查了 35 个村庄,首先通过调查的方式(比如问你你曾拜访过谁,谁曾拜访过你等问题)描绘出了每个村庄的社交网络结构(\(g\))。然后问了两个问题来统计村民心目中谁是八卦之王:1. 如果你有一个贷款产品你想告诉村子里每一个人,你会告诉谁?2. 如果有演出消息你想告诉村子里每个人,你会告诉谁?这样,作者就获得了每个村庄的“八卦之王”的提名以及排序。
此外,作者还把商店老板、教师等与其他人接触较多的个体单独列出来作为“leaders”,因为这些人是天然的“八卦之王”候选人(仿照 Bharatha Swamukti Samsthe 的做法)。
首先,比较一下被提名的人以及 leaders 的分布:
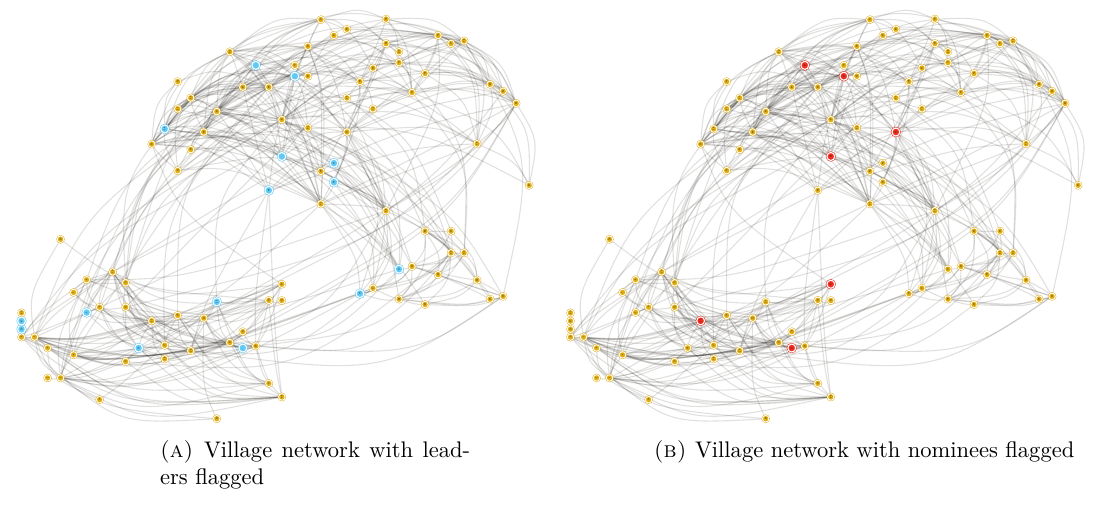
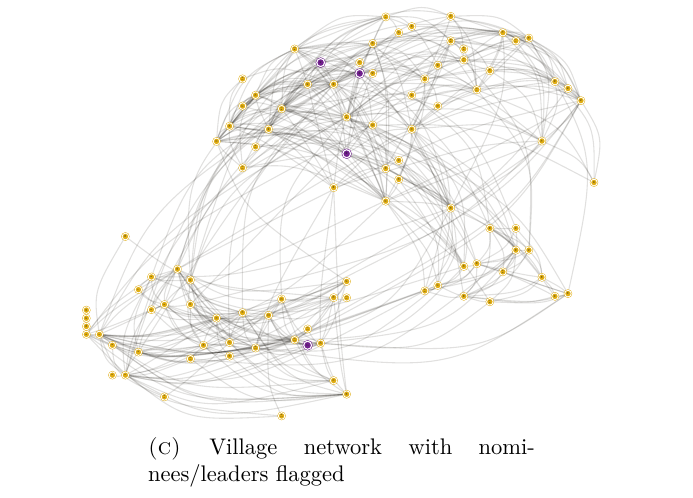
可以发现,(A) 中的 leaders 更容易包括很多不重要的人物,而 (B) 中的排名看起来更靠谱一点。
既然有了网络的信息,就可以计算一下特征值集中度,然后看看村民报告的“八卦之王”跟理论计算出来的特征值集中度是不是一致的:
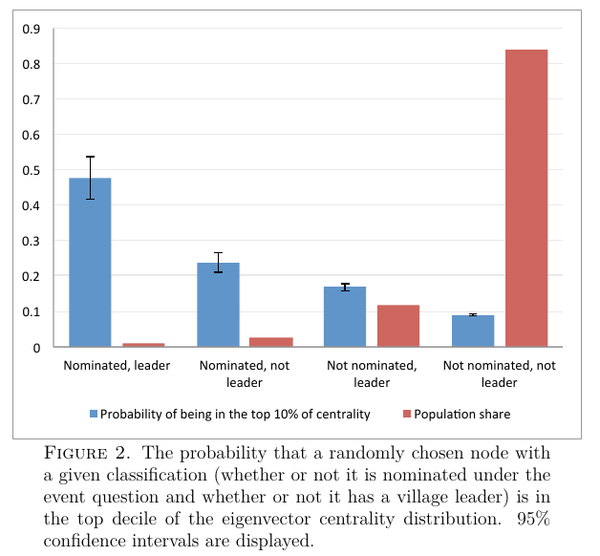
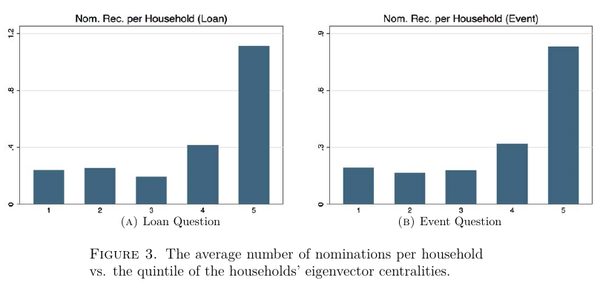
可以发现,通过特征向量集中度计算的“八卦之王”更容易被村民提名(上图),而且被提名的也更多的出现于特征向量集中度更高的人群(下图)。
当然,这种比较太过于粗略。村民可能仅仅报告那些有更多朋友的人,或者地理位置上更方便传播消息的人,所以作者还做了回归分析,通过控制其他的变量,看前面的DC集中度是不是能更好的预测被提名的概率(次数):
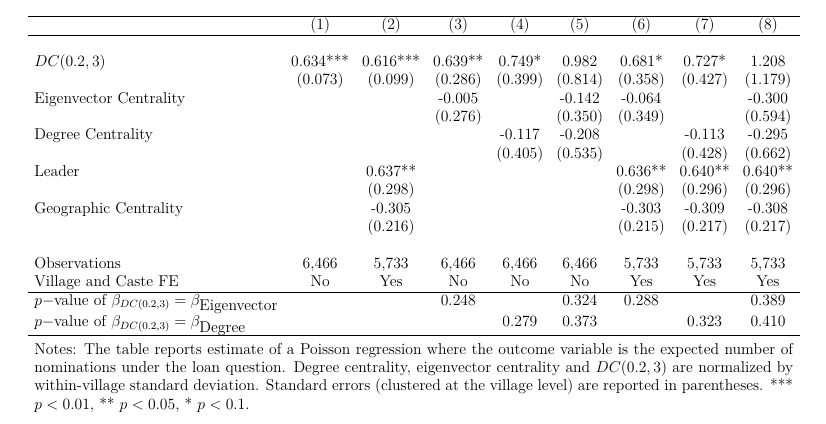
至于回归结果吗,大家看看就好,作者的DC集中度一开始很显著吗,但是随着控制其他变量,显著性水平越来越差,虽然系数值越来越大。但是作者指出,如果做三个集中度变量的联合检验,联合起来却是显著的。问题可能出现在三个变量的共线性上(这也就是我一直强调的,共线性怎么办?没办法,看大神写文章是顺着写的,一开始变量少,慢慢增加变量,而不是相反,怀疑有共线性了再删变量)。
所以呢,你看,村民都是有这种能力的~
慧航:我对这个领域不是特别熟,我是追着 duflo 看的这篇文章,这个数据我也是第一次看到。
杨张博:请问 duflo 是哪个领域的啊?各种中心度的共线性应该是天然的,都是从 degree 这个基本概念推导出来的。另外,我看这篇论文用的是 possion 回归,但是网络数据回归是否有效一直存在争论。Jackson 在他的课上也讲了基于随机图的方法,但奇怪的是在这篇文章中没有用。
慧航:经济学领域的大神,这篇文章主要是理论贡献吧,后面的 poission 回归只是说明理论的预测是合乎现实的,可能不同学科做 social network 关注的点不一样吧。
养猪就用金坷垃:我其实不太明白他后面做回归加变量干什么,因为如果你加的是无关或者弱相关的变量,很明显会干扰原来的变量,造成显著水平变差啊?
慧航:如果加的是无关的变量,是不会干扰原来的变量的,不信你推一下
养猪就用金坷垃:恩,应该是有相关性。但是对这篇论文来说,相关性完全不是问题啊。因为本来就是创造出一个指标来统计八卦指数,那和其他因素相关也无所谓啊。反倒正好说明这个指数和其他包含了各种因素。
慧航:我觉着这篇文章的意义不是创造一个指数,而是证明了社交网络中的个体都有能力知道谁是这个社交网络中的关键先生。