原文地址:https://zhuanlan.zhihu.com/p/19931167
学过线性回归的同学肯定都学过\(R^2\),而且老师都会告诉你们,\(R^2\)是评判一个模型拟合好坏的重要标准。但是我在上高级计量经济学课的时候,老师首先就告诉我们,\(R^2\)是一个很不靠谱的东西,不能把这个作为评判模型的依据。而这一点也在不同课程、不同老师那里得到了印证。
为什么要重新提出这个问题,主要是在线性回归中的 ANOVA 的作用是什么? - 方差分析和方差分析和回归分析的异同是什么? - 统计学这两个问题里面跟某些人发生了一些争执。
如果你去看这两个题目,首先有一点需要注意的是,第一个问题里面的 ANOVA 指的是做完线性回归之后汇报出来的那个方差分析表,跟后面的方差分析还不完全是一回事。做完线性回归之后的那个ANOVA表主要是用来计算\(R^2\)的,这一点可以看我的答案方差分析和回归分析的异同是什么? - 慧航的回答
那么,为什么我说在计量经济学领域,\(R^2\)是个不靠谱的指标呢?因为计量经济学关注的是解释变量究竟是怎样解释被解释变量的,而拟合的好坏,多数情况下我们并不关心。
为了说明这一点,我做了几个数值模拟告诉大家:
clear
set more off
set obs 1000
gen z=rnormal(0,1)
gen z2=rnormal(0,1)
gen x1=z+z2
gen x2=z2+rnormal(0,1)
gen y=-1*x1+2*x2+rnormal(0,1)
gen y2=-1*x1+2*x2+3*rnormal(0,1)
*********** different error terms**********
reg y x1 x2
reg y2 x1 x2
*********** transformation ******
gen yp=y-3*x1
reg y x1 x2
reg yp x1 x2
*********** IV, negative R-square *******
reg y x1
ivregress 2sls y (x1=z)以上是用 Stata 写的,非常简单。我们先来比较第一组结果,也就是
*********** different error terms**********
reg y x1 x2
reg y2 x1 x2结果如下:
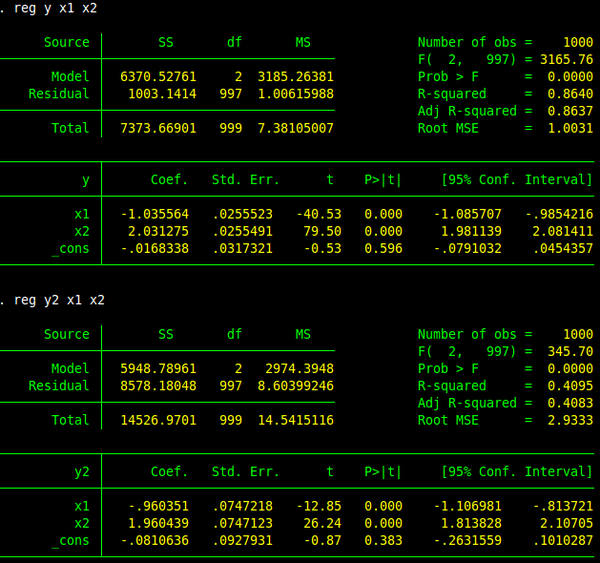
两个回归的差别仅仅在于,第二个方程的扰动项的方差是第一个的 3 倍,导致\(R^2\)从 86.4% 下降到了 40.95%,于是我们可以得到一个结论:\(R^2\)度量的是你未观察到的部分与观察到的部分的方差,而如果我们的兴趣点在与\(x\)对\(y\)的影响,那么再小的\(R^2\)也不代表模型的解释能力弱。
下面我们来比较第二组结果,也就是:
*********** transformation ******
gen yp=y-3*x1
reg y x1 x2
reg yp x1 x2结果如下:
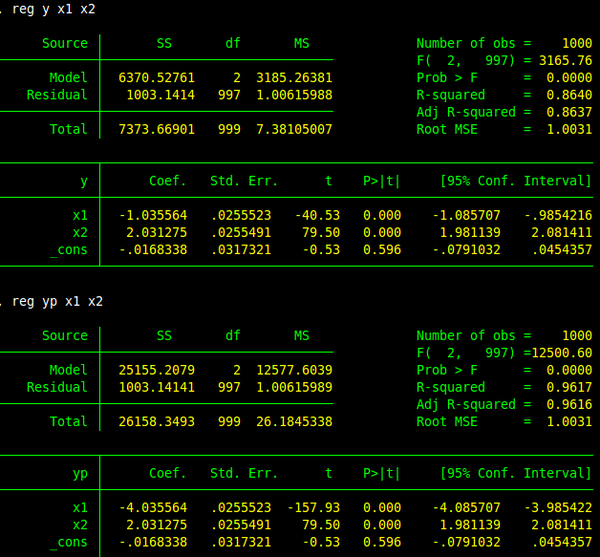
可以看到,我仅仅是在\(y\)上减去了\(3x_1\),的到的\(R^2\)就从 86.4% 上升到了 96.17%。我们可以证明,第二个方程的估计结果应该是和第一个方程的估计结果一模一样的(\(x_1\)的系数要加上 3 之后一模一样),连 standard error 也一模一样,说白了,这两个是同一个回归,但是,\(R^2\)却差别很大。请问这样的\(R^2\)的上升有意义么?
最后一组,也是最 amazing 的:
*********** IV, negative R-square *******
reg y x1
ivregress 2sls y (x1=z)回归结果:
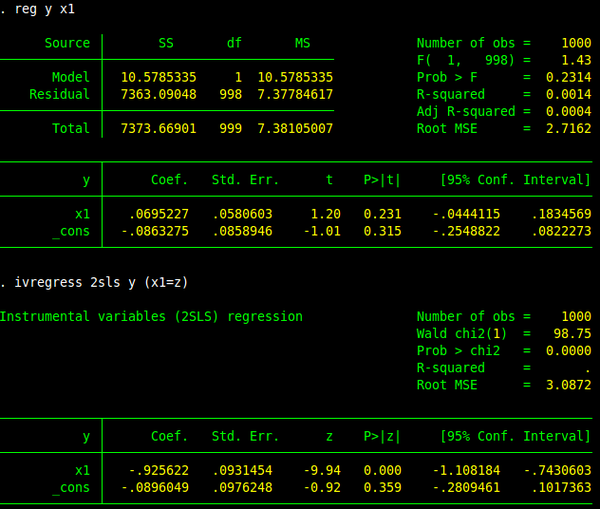
如果仔细看我的数据生成过程,我做回归忽略了\(x_2\),自然导致了内生性的问题,所以 OLS 的回归结果是有误导性的,不对的。解决办法是用 IV 的方法,也就是下面的回归结果,回归系数与真实值(-1)差别不大。但是你仔细看一下,IV 的回归结果里面没有报告\(R^2\),知道为什么么?因为经过我精巧的设计,你会发现,在这个例子里面,IV 估计的\(R^2<0\)。但是从计量经济学的观点哪个估计好呢?IV 的估计好,因为 IV 的估计准确的告诉了你\(x_1\)对\(y\)的影响。
综上,在我们做完回归的时候,\(R^2\)高并不代表我们的回归方程解释能力强,\(R^2\)低也不代表我们的回归解释能力就差。用\(R^2\)来评判回归,至少在计量经济学里面,是比较业余的。
p.s. 最后补充一条,我说计量经济学里面\(R^2\)不重要,不是说这个东西完全没用。比如当我们做收入不平等问题的时候,多少不平等来自于观察到的差距、多少来自观察不到的等等,\(R^2\)和 ANOVA 表格还是非常有用的。但是多数情况下,拿\(R^2\)评判别人的模型是非常业余的行为。
下面这段是给 @weixin shi 科普的,证明在此:
命题:有截距项的 OLS,其\(R^2\geq 0\)。
证明:

炒鸡简单的一个证明。看不懂不要问我了。我不用问我计量老师,我本身就是半个计量老师。如果你计量老师告诉你这条定理不对,我真担心你们学校的老师质量差的可以。