1 冉筱韬 (随机实验，自然实验)

「因果识别」可以算得上是社会科学实证研究里的核心问题了。首先来定义一下什么叫做「因果关系」。

举一个例子来说明：读大学并拿到本科学位对收入有什么影响？（这里要注意的一点是，类似于「影响」，「效果」，或者英文里的 impact, effect, lead to, result in 一类的词都代表着你在描述的是因果关系。使用的时候要非常小心。）

• 对于某个特定的个人，我们需要知道两件事：(1) 这个人读大学并拿到本科学位之后的收入；(2) 让这个人穿越回要上大学之前的那个节点，不上大学，直接去工作的收入。用(1)减去(2)就是这个人读大学并拿到本科学位对他(她)本人收入的影响。
• 对于某群人，我们同样需要知道两件事：(1) 这群人读大学并拿到本科学位之后收入的均值；(2) 让这群人都穿越回各自上大学之前的节点，不上大学，直接去工作的收入的均值。同样用(1)减去(2)。

所以想要得到因果识别的结果，最关键的一点就是得到对照组（counter-factual），也就是上面列出的(2)代表的结果。

自然科学可以通过实验环境创造出比较可信的对照组，而社会科学的困境就在这里。我们研究的主体是人和人的行为，很难找到两个各方面指标都一致的人互为对照组，而实验也非常难以严密控制。如果有时光机，可以穿越，搞社会科学实证研究的大概都会喜极而泣吧。

所以总结起来，各种「因果识别」的方法本质上都是在寻找可信的对照组。

至于现在主流的常用的方法，@张译文的答案已经写的蛮全了。我这里做一些补充说明，顺便也是给自己读过的文献做个梳理。举的例子主要是劳动—教育经济方面的，角度会比较偏向政策分析。有重复的地方还请见谅哈。

2 Manolo (充分统计量)

@冉筱韬、@慧航等大神的答案已经十分详尽了。这里补充一个近年来在公共经济学，尤其是税收、社保领域用得比较多的方法：充分统计量（Sufficient Statistics）。以下内容全部来自Chetty在2008年完成的关于充分统计量方法的综述。

上图描述了充分统计量的工作机理。我们知道，识别方法有structural和reduced两个门派，前者要建模型，然后去估计其中的所有参数；后者则是通过做实验或者设法构造类似实验得到的数据，通过种种回归得到结果。充分统计量实际上是两者的折衷。以税收政策为例，虽然我们可能也很关心税收变动对商品产量、顾客需求等变量的影响，但说到底，我们最关心的还是社会的整体福利。如果我们能够把社会福利变动表达成其它一些容易估计的量的函数，事情就会好办很多。这种方法既有reduced form容易估计、假设相对少的优点，也有一部分structural form的优点：可以做政策模拟和预测。

Chetty在论文开头使用了Harberger在1964年AER发表的经典论文的简化版作为例子来说明这种方法，我也录在这里。这个方法必须要有实例才能明白其强大。如果为公式所困扰，可能没有什么好办法，因为充分统计量的实质就是找到巧妙的方法去简化模型，从模型中显式地解出我们需要的那些变量。假设经济体中有一种计价物\(y\)和\(J\)种消费品，生产商品需要投入\(y\)，成本函数为\(c(x_{i})\)。记消费者的消费向量是\(\pmb{x}=(x_{1},..., x_{J})\)，经济体中的价格向量是\(\pmb{p}=(p_{1},..., p_{J})\)，假设消费者效用函数取拟线性形式，并面对总数为\(Z\)的收入约束。当政府对商品\(x_{1}\)征收税率为\(t\)的比例税时，我们得到如下优化问题，其中待优化变量都是\(\pmb{x}\)。

消费者：

\[ \begin{aligned} \max u(x_{1},..., x_{J})+y\\ s.t. p\pmb{x}+tx_{1}+y=Z \end{aligned} \]

生产者：

\[ \max p\pmb{x}-c(\pmb{x}) \]

利用生产=消费这一约束条件可以闭合以上优化问题。如果我们直接求解然后再去估计税收的影响，比如像Deaton和Muellbauer他们做的那样，这就是个structural的问题。但是，如果只是为了得到税收对福利的影响，这里完全没有必要去求解模型。直接写出社会福利的表达式，代入约束，我们得到如下结果：

\[ \begin{aligned} W(t) &= \left\{ \max u(x_{1},..., x_{J})+Z-p\pmb{x}-tx_{1} \right\} +\left\{\max p\pmb{x}-c(\pmb{x}) \right\} +tx_{1}\\ & = \left\{ \max u(x_{1},..., x_{J})+Z-tx_{1}-c(x) \right\} +tx_{1} \end{aligned} \]

两边对\(t\)微分，再利用包络定理，我们得到：

\[ \frac{dW(t)}{dt} =-x_{1}+ x_{1}+t\frac{dx_{1}}{dt} =t\frac{dx_{1}}{dt} \]

从这里可以看到，我们可以把福利的变动写成\(\frac{dx_{1}}{dt}\)和\(t\)相乘的简单形式。假设原有税率为\(t\)，新的税率是\(t'\)，在得到\(\frac{dx_{1} }{dt}\)的估计值，亦即需求的变动之后，我们就可以通过计算\(\int_{t}^{t'} t\frac{dx_{1} }{dt} dt\)来得到税收对福利的影响，以上就是运用充分统计量方法的一般流程。尽管在实际操作中问题通常没有这么简单，但方法是相通的。以下是Chetty整理的近年来利用充分统计量方法的文献，可以选择阅读。其它一些更高级的应用同样请参见这篇文献。

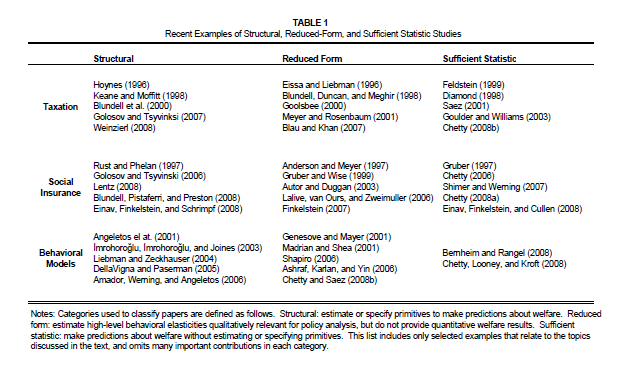
最后还需要强调一点：充分统计量在折衷两派，汲取各自优点的时候，也同时保留了两边的一些缺点。

• 首先，因为统计量的推导基于结构模型，如果模型设定有误，统计量的正确性也得不到保证。
• 其次，这样估计得到的结果在外推时不一定有效。最后，我们得到的估计实际上是个黑箱，比如说上面的例子，我们只能看到福利的变动，但影响福利变动的那些参数，我们一个都看不到。由于有充分统计量就有模型，Chetty对此给出的建议是在研究时既做structural，也做充分统计量，这样可以最大程度发挥二者的长处。

参考文献：Chetty R, Fort M, IZA C. Sufficient Statistics for Welfare Analysis A Bridge Between Structural and Reduced-Form Methods[J]. Annual Review of Economics, 2009, 1: 451-488.

3 知乎用户 (流行病学，详细)

居然没有人关注流行病学在causal inference当中的贡献……流行病学才是完完全全聚焦于因果推断的学科啊！我个人博士一年级在本系接受的都是计量经济学和社科那一路的训练，但后来在上过两年完整的流行病学方法后，现已经完全被流病洗脑。

改一篇旧文讲讲这件事~

因果关系本身，理论上本来就不容易搞清楚，在研究中如何呈现也都很难。所以因果推断在流行病学，以及各类依靠因果关系吃饭的社科里，比如计量经济学，都很令人头疼。当然我曾经看到有人吐槽说：现在社会学里为什么还有人搞因果关系，搞因果关系的人都该剖腹自杀。我的确不明白此人为何这样说，如果那样的话，首先剖腹自杀的是我们整个公卫界，尤其是全体流行病学家，顺带自杀的应该还有计量经济学家等。另外，因果推断这套东西，归根结底是empiricism这一路线之下的困惑，毕竟相关问题的提出最早可以追溯到Hume。所以非这一路线的人自然很难认可因果这种说法，及其衍生讨论。这种路线之争我也就不自己挖坑跳了。（譬如曾经有人类学现象学一脉思路的朋友跟我说，譬如我自己心中种种微妙感受，和社会大环境又有什么关系，又如何梳理得出因果关系？）

目前流行病学界比较接受的因果关系的定义是和counterfactual effect密切相关的。这个坑爹词汇到底啥意思呢？曾经有个蛋疼的流行病学家写了一篇论文讨论希腊诸神参与的临床试验。在论文中，希腊诸神参与了一次标准的随机对照试验，一半的神被分到试验组，一半的神被分到对照组。之后我们可以得到两组众神的死亡率。这些神和我们广大凡人一样，在接受治疗时可能有四种情况：不治不能好但治了能好，不治不能好治了也不能好，不治能好治了也能好，不治能好治了反而不能好。神毕竟是神，所以我们可以知道他们治了以及没治两种情况的后果，从而得出诸神治了之后的死亡率，以及诸神没治的死亡率。这两个死亡率的差，才是治疗的效果（effect）。

但是凡人毕竟不是神，我们要么治了，要么没治，有的路走了就不能回头，我们用法无法获知没走这条路时我们会是什么模样。所以我们永远只能对比治了和没治的人，而无法对比所有人治了之后的结局和所有人没治的结局。对于个体来说，你获得治疗之后的后果，就是事实（factual）的情况，而你没有获得治疗之后的后果，就是反事实（counterfactual）的情况。因果关系的标准定义就是事实后果和反事实后果的差异。

当然，根据这个定义，如果没有更多的假设，我们将永远无法获知因果关系。因为，我们永远无法获知反事实的后果究竟会怎样。而我们在现实中所得到的将永远只是关联（association）而已。 但如果我们加上某些假设，我们在现实研究中所获得的关联，能够迫近因果的效应么？ Yes, we can.

但我们的代价是两个无法验证的基本假设：

1. 你所观察的，就是实际上发生的。如果发生白大褂效应这种悲剧，那么你将永远无法迫近真相。(流病老师的原话是：BAD LUCK!)
2. 你已经控制了所有confounding（混杂）。但是你永远无法确认这一点，因为没有任何统计检验以及数据的模样可以告诉你这一点。

虽然这两点我们无法验证，但没有这两点，我们都可以回家了。（流病老师原话）

在流行病学家喜欢的Pearl路线中，用所得到的关联，去迫近因果的过程叫做：identification。但这也是有条件的，不是所有情况都可以找到因果关系，某些时候，你必须要承认，即便你做到完美，你还是不行。而这个过程不外乎两条路，走前门儿（front door criteria），或者走后门儿（back door criteria）。若想搞清楚走前门儿和走后门儿的准确涵义，需要顺便搞清楚DAG（directed acyclic graph）以及对应的概率表达和结构模型，在此省略一万字。

一般来说，大家常用的路线都是争取符合back-door criteria，那就是控制confunding。当然控制confounding的方式有很多，譬如以上许多答案提到的RCT，再譬如现在社科很喜欢的Natural experiment（可参考《Natural Experiments in the Social Sciences: A Design-Based Approach》）。从DAG的视角来看，随机化本质上也是一个工具变量。之前发在NEJM上关于Oregon医保试验（Medicaid抽签）的文章既是一个RCT的设计，同时分析中也将随机化的结果用作工具变量。而Regression Discontinuity之类方法本质上也是natural experiment的路线，因为目标是要追求暴露分布（或者说干预实施）as if random的效果。当然，如果大家只有观察性数据，不能在研究设计上动脑筋的话，就要在别处动脑筋了。譬如，Pearl想出了front-door criteria。再譬如，社科中常用的propensity score，还有inverse probability weighting，doubly/multiple robust estimation。实在实在不行，就要走上simulation和bias analysis的道路了。

其实以上这两点假设，还有一个隐藏假设：我们没有测量偏倚以及选择偏倚，只有混杂。如果有测量偏倚和选择偏倚，我们的处理方法会更加复杂（流行病学家把所有的偏倚分为三类：混杂、选择偏倚、测量偏倚）。

总体来说说，流行病学家对于计算机、统计、计量经济学领域的因果推断进展吸纳得非常充分，也做出了自己的贡献。但是流行病学家整体来说不太使用structural equation modeling (SEM)，除了学科训练的壁垒，还有一些对SEM方法上的顾虑（参考Vanderweele那篇：structural equation models and epidemiologic analysis）。

知乎用户：一切皆因果，因子太多，结果不明确，导致了整个关系显的复杂。

大象：因为sem是用来做成熟理论框架下的estimation，流行病学或者说医学缺少理论框架，dag还只停留在representation的层面上，如果在卫生经济学里面可能会有所使用吧。就像hastie那本书里说，数据出发能得到无穷多种假设，你要么预设理论，让data来选择模型，要么预设模型，让data来选择理论，sem是前者，我们流行病往往是后者。

4 慧航 (同群效应有一个问题)

谢邀。之前各位已经写了很多很有启发的答案了，最近比较忙，积攒了很多问题没有回答，先行道歉。

在这里我总结一下计量经济学的门派吧，然后再说经济学中的因果识别方法，希望这个答案能在一个稍微大一点的视角做一点总结。

首先大家应该一下子就能想到，计量经济学首先有两个大的门派，微观计量和宏观计量。前者一般从微观个体出发，后者更多应用时间序列数据。当然，宏观经济学用到的方法，除了计量经济学的估计和识别之外，还有校准，这个我不是很熟，就不多说了。

而无论是哪个门派，下面又有很多宗派。比如在宏观计量里面，传统的matching moment、MLE和现在非常流行的Bayesian显然是两个不同的宗派。而在微观计量里面，则区分了structural-form和reduced-form两个宗派。

题主问的是因果识别，那我们就先来说一下不同门派、宗派之间因果识别的差别。

首先说我最不擅长的宏观计量。宏观方面，最popular的概念应该是格兰杰因果了。但是，相信大家都听说过，格兰杰因果不是真的因果。格兰杰意义上的因果仅仅是看滞后的变量能不能预测当期的变量，这里面问题就很多了。在这一领域，传统的方法是VAR，以及相应的VECM等，格兰杰因果也是在这个框架里面的东西。但是如果真的想要识别因果，特别是有当期影响的时候，就需要用SVAR了。

微观计量呢？微观计量的因果识别好玩的多。结构和简约两个门派总在相互竞争中不断发展新的想法。两者的区别在于，结构模型有有力的理论模型作为支撑，目的是估计模型的结构参数。而简约派则是避开复杂的经济理论建模和结构参数的估计，通过使用自然实验、工具变量等方法直接找到想要的参数（这个有点像唯识宗给你丝丝分析宇宙人生，而禅宗则是明心见性，直指人心）。

在举例子之前，我先总结一下以上答案提到的方法：

• OLS、实验：最基本的办法，除非有理论支撑，或者数据来自与实验数据，一般会失败。
• IV：当存在内生性的时候普遍的解决办法，很多方法，比如RD、LATE都可以看作是IV
• DID：自然实验，实验组和控制组有共同趋势
• RD：自然实验，外生的断点

以上的这几个方法都是reduced-form最经常用的。其中OLS和IV因为太general，所以structural model也会大量使用（在structural模型里面，IV经常是系统内部就可以找到的）。当然，对于structural model中足够复杂的模型，MLE、GMM以及许许多多其他估计方法都是非常多的。

为了更直观的给大家说清楚两个宗派的差别，我举个例子，如何识别peer effects。这套文献说白了就是想要看人和人之间的交互影响，比如你努力学习会不会影响到你的朋友也努力学习。首先我们来看structural-form怎么做的（Peer Effects and Social Networks in Education, Calvo-Armengol, Patacchini and Zenou, The Review of Economics Studies.）：

• 第一步，理论建模：

• 第二步：讨论均衡

• 第三步：讨论识别条件

• 最后，得到估计。

这里我就截屏略过具体的细节了，只想给大家看一下structural model是怎么做的，具体感兴趣可以看原文。

那么同样一个问题，reduced-form是怎么做的呢？Peer Effects in Program Participation, Gordon B. Dahl, Katrine V. Loken and Magne Mogstad, The American Economic Review给出了一个用RD来识别peer effects的例子(感谢 @zc deng 的slides)。

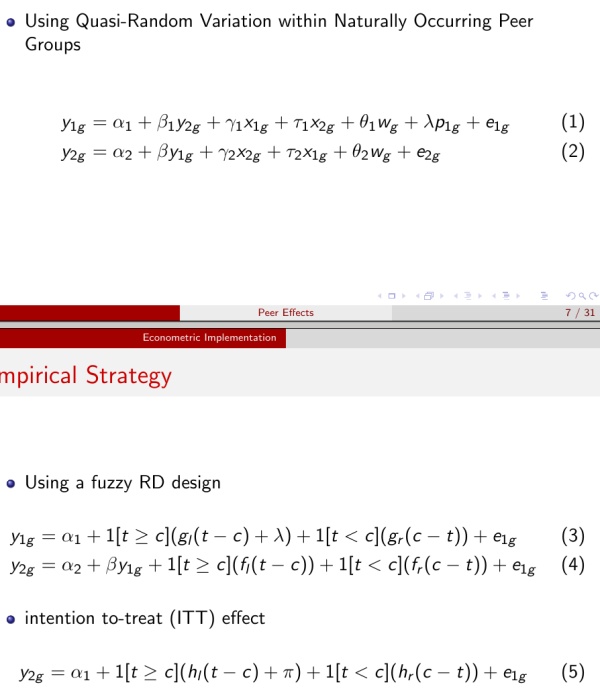
Peer effects的识别有个很严重的问题是reflection problem，也就是相互影响。而这篇文章使用了休产假的改革作为自然实验，巧妙的避开了这个问题。这篇文章没有像前一篇文章那样复杂的理论建模，自然实验的背景一下子把问题简化了许多。而在第一篇文章里面，这个问题则是在给出理论假设的条件下给出识别的。

现在，问题来了：拳有南北，国有南北么？

哈哈，开个玩笑。有段时间，看文献的时候也会问，究竟哪个宗派更好。直到后来，我才发现我多虑了。在没有达到一定的水平之前，讨论自己归属什么宗派，总是有点自不量力的感觉。就好像有人问我是禅宗还是净土宗，我说按照我的修为，还到不了谈宗派的程度。

宗派归属可以不谈，但是宗派之间的差别却是可以谈的。前面说了宗派之间的差别，那么，两个宗派之间有没有联系呢？下面是私货时间，我自己的想法，不喜欢请轻喷。。。

我觉着，是有的。之前说的什么RD DID都是招式，但是仔细考虑下来，经济学的识别方法无非就两个：找实验、加假设。

这两个东西，一个是数据的问题，另外一个，则是理论的问题。

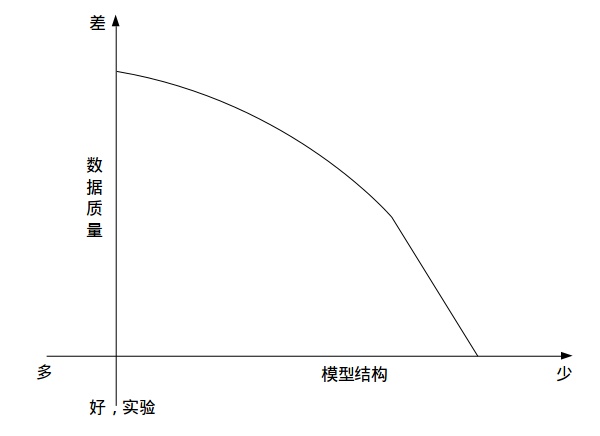
最理想的情况，是你有实验数据。这个时候，啥都不用多想，OLS就可以解决问题。但是多数情况下，你没有那么好的数据，这个时候，可以退而求其次，找一些自然实验。比如RD，虽然你的数据不是实验数据，但是由于有外生的断点，你只需增加一个假设，那就是其他变量在断点处没有断点，那么，你还是可以在局部识别出你想要的东西。但是，如果你连自然实验都没有，那麻烦就大了。你不得不增加更多的假设，然后你会发现，你的模型慢慢的变成了structural model。

再举一个例子，我想做教育的回报，比如上大学对未来收入的影响。最好的情况，是我做一个实验，找一批孩子，随机让他们上大学或者不上大学，几年之后看他们收入的差距，这是最理想的情况。如果不能做实验，那么退而求其次，我们看看有没有自然实验。比如某次考试高于某个分数的可以上大学，低于这个分数不能上大学，那么好了，我们可以做一个RD，看在这个分数线周围的学生有没有明显的工资差异。如果连这个都没有，那么我可能需要找IV，这个时候你就需要假设你的IV是外生的，而找IV也是个非常艰难的过程。最后，如果你IV也找不到，还有方法是你把上不上大学这个行为也进行建模，然后在这个模型里面加入一些很强的假设（比如方程之间误差项的分布、相关性等），通过这些假设，也可以作出结果。以上的这个过程，随着你的数据越来越差，假设也越来越强，模型也越来越结构化（你需要添加更多的结构）。

其实在宏观计量里面也是这样。比如前面提到的SVAR的识别，一般来说模型很难识别，为了识别这个模型，许许多多可能的假设被加到这个模型里面，使得最后这个模型可以被识别。比如一开始的时候，大家在误差项里面做假设，使得参数可以被识别。后来大家又直接根据宏观理论，假设某些系数的符号，给出识别，或者假设某些参数的值为0给出识别。这个过程跟上面的想法是一样的，如果不能识别，做假设也得把模型识别出来。至于怎么做假设，就看你的理论模型了。

所以，很多时候不是我们去选择用哪个宗派，而是手中的数据决定的。或者说，我们总是在假设和数据之间做trade-off。当然假设是不是合理，那是另外一回事，文章的好坏也跟假设是否合理有直接关系。

扯了这么多，无非是想说，其实因果识别的方法很多，大家列举出来的和大家没有列举出来的，总会有一些共性。答案有点杂，排版有点乱，时间关系，就先写这么多吧，这里面有太多东西可以写，这么一个答案显然是不能给出因果识别的全貌的。此外，如果有错误，请提出更正，欢迎讨论。

另外，大家还忽略了一个问题，就是关于因果，何谓因果，在学术界还是有一些争议的，这点过几天可能会在另外一个答案里面详细描述，暂时不做讨论。

最后，以上给了这么多废话，最后给一点干货吧，除了Angrist的《人畜无害的计量经济学》，有本书特别推荐阅读：Micro-Econometrics for Policy, Program, and Treatment Effects, MYOUNG-JAE LEE作为一本专门讨论treatment effects的书，很值得阅读。

5 匿名用户 (回归，机器学习，Rubin，结构模型，充分统计量)

经济学中主要有五种 approach：

• 多元线性回归（multiple linear regression）
• 机器学习（machine learning）
• Rubin 因果模型（Rubin’s casual models）
• 结构模型（structural models）
• 充分统计量（sufficient statistics）

下面转载 Kevin Bryan 的一篇文章，对于这些方法以及各自存在的问题介绍的比较清楚：

“Does Regression Produce Representative Estimates of Causal Effects?,” P. Aronow & C. Samii (2016) by Kevin Bryan on February 26, 2016 A “causal empiricist” turn has swept through economics over the past couple decades. As a result, many economists are primarily interested in internally valid treatment effects according to the causal models of Rubin, meaning they are interested in credible statements of how some outcome Y is affected if you manipulate some treatment T given some covariates X. That is, to the extent that full functional form Y=f(X,T) is impossible to estimate because of unobserved confounding variables or similar, it turns out to still be possible to estimate some feature of that functional form, such as the average treatment effect E(f(X,1))-E(f(X,0)). At some point, people like Angrist and Imbens will win a Nobel prize not only for their applied work, but also for clarifying precisely what various techniques are estimating in a causal sense. For instance, an instrumental variable regression under a certain exclusion restriction (let’s call this an “auxiliary assumption”) estimates the average treatment effect along the local margin of people induced into treatment. If you try to estimate the same empirical feature using a different IV, and get a different treatment effect, we all know now that there wasn’t a “mistake” in either paper, but rather than the margins upon which the two different IVs operate may not be identical. Great stuff.

This causal model emphasis has been controversial, however. Social scientists have quibbled because causal estimates generally require the use of small, not-necessarily-general samples, such as those from a particular subset of the population or a particular set of countries, rather than national data or the universe of countries. Many statisticians have gone even further, suggestion that multiple regression with its linear parametric form does not take advantage of enough data in the joint distribution of (Y,X), and hence better predictions can be made with so-called machine learning algorithms. And the structural economists argue that the parameters we actually care about are much broader than regression coefficients or average treatment effects, and hence a full structural model of the data generating process is necessary. We have, then, four different techniques to analyze a dataset: multiple regression with control variables, causal empiricist methods like IV and regression discontinuity, machine learning, and structural models. What exactly do each of these estimate, and how do they relate?

Peter Aronow and Cyrus Samii, two hotshot young political economists, take a look at old fashioned multiple regression. Imagine you want to estimate y=a+bX+cT, where T is a possibly-binary treatment variable. Assume away any omitted variable bias, and more generally assume that all of the assumptions of the OLS model (linearity in covariates, etc.) hold. What does that coefficient c on the treatment indicator represent? This coefficient is a weighted combination of the individual estimated treatment effects, where more weight is given to units whose treatment status is not well explained by covariates. Intuitively, if you are regressing, say, the probability of civil war on participation in international institutions, then if a bunch of countries with very similar covariates all participate, the “treatment” of participation will be swept up by the covariates, whereas if a second group of countries with similar covariates all have different participation status, the regression will put a lot of weight toward those countries since differences in outcomes can be related to participation status.

This turns out to be quite consequential: Aronow and Samii look at one paper on FDI and find that even though the paper used a broadly representative sample of countries around the world, about 10% of the countries weighed more than 50% in the treatment effect estimate, with very little weight on a number of important regions, including all of the Asian tigers. In essence, the sample was general, but the effective sample once you account for weighting was just as limited as some of “nonrepresentative samples” people complain about when researchers have to resort to natural or quasinatural experiments! It turns out that similar effective vs. nominal representativeness results hold even with nonlinear models estimated via maximum likelihood, so this is not a result unique to OLS. Aronow and Samii’s result matters for interpreting bodies of knowledge as well. If you replicate a paper adding in an additional covariate, and get a different treatment effect, it may not reflect omitted variable bias! The difference may simply result from the additional covariate changing the effective weighting on the treatment effect.

So the “externally valid treatment effects” we have been estimating with multiple regression aren’t so representative at all. So when, then, is old fashioned multiple regression controlling for observable covariates a “good” way to learn about the world, compared to other techniques. I’ve tried to think through this is a uniform way; let’s see if it works. First consider machine learning, where we want to estimate y=f(X,T). Assume that there are no unobservables relevant to the estimation. The goal is to estimate the functional form f nonparametrically but to avoid overfitting, and statisticians have devised a number of very clever ways to do this. The proof that they work is in the pudding: cars drive themselves now. It is hard to see any reason why, if there are no unobservables, we wouldn’t want to use these machine learning/nonparametric techniques. However, at present the machine learning algorithms people use literally depend only on data in the joint distribution (X,Y), and not on any auxiliary assumptions. To interpret the marginal effect of a change in T as some sort of “treatment effect” that can be manipulated with policy, if estimated without auxiliary assumptions, requires some pretty heroic assumptions about the lack of omitted variable bias which essentially will never hold in most of the economic contexts we care about.

Now consider the causal model, where y=f(X,U,T) and you interested in what would happen with covariates X and unobservables U if treatment T was changed to a counterfactual. All of these techniques require a particular set of auxiliary assumptions: randomization requires the SUTVA assumption that treatment of one unit does not effect the independent variable of another unit, IV requires the exclusion restriction, diff-in-diff requires the parallel trends assumption, and so on. In general, auxiliary assumptions will only hold in certain specific contexts, and hence by construction the result will not be representative. Further, these assumptions are very limited in that they can’t recover every conditional aspect of y, but rather recover only summary statistics like the average treatment effect. Techniques like multiple regression with covariate controls, or machine learning nonparametric estimates, can draw on a more general dataset, but as Aronow and Samii pointed out, the marginal effect on treatment status they identify is not necessarily effectively drawing on a more general sample.

Structural folks are interested in estimating y=f(X,U,V(t),T), where U and V are unobserved, and the nature of unobserved variables V are affected by t. For example, V may be inflation expectations, T may be the interest rate, y may be inflation today, and X and U are observable and unobservable country characteristics. Put another way, the functional form of f may depend on how exactly T is modified, through V(t). This Lucas Critique problem is assumed away by the auxiliary assumptions in causal models. In order to identify a treatment effect, then, additional auxiliary assumptions generally derived from economic theory are needed in order to understand how V will change in response to a particular treatment type. Even more common is to use a set of auxiliary assumptions to find a sufficient statistic for the particular parameter desired, which may not even be a treatment effect. In this sense, structural estimation is similar to causal models in one way and different in two. It is similar in that it relies on auxiliary assumptions to help extract particular parameters of interest when there are unobservables that matter. It is different in that it permits unobservables to be functions of policy, and that it uses auxiliary assumptions whose credibility leans more heavily on non-obvious economic theory. In practice, structural models often also require auxiliary assumptions which do not come directly from economic theory, such as assumptions about the distribution of error terms which are motivated on the basis of statistical arguments, but in principle this distinction is not a first order difference.

We then have a nice typology. Even if you have a completely universal and representative dataset, multiple regression controlling for covariates does not generally give you a “generalizable” treatment effect. Machine learning can try to extract treatment effects when the data generating process is wildly nonlinear, but has the same nonrepresentativeness problem and the same “what about omitted variables” problem. Causal models can extract some parameters of interest from nonrepresentative datasets where it is reasonable to assume certain auxiliary assumptions hold. Structural models can extract more parameters of interest, sometimes from more broadly representative datasets, and even when there are unobservables that depend on the nature of the policy, but these models require auxiliary assumptions that can be harder to defend. The so-called sufficient statistics approach tries to retain the former advantages of structural models while reducing the heroics that auxiliary assumptions need to perform.

Aronow and Samii is forthcoming in the American Journal of Political Science; the final working paper is at the link. Related to this discussion, Ricardo Hausmann caused a bit of a stir online this week with his “constant adaptation rather than RCT” article. His essential idea was that, unlike with a new medical drug, social science interventions vary drastically depending on the exact place or context; that is, external validity matters so severely that slowly moving through “RCT: Try idea 1”, then “RCT: Try idea 2”, is less successful than smaller, less precise explorations of the “idea space”. He received a lot of pushback from the RCT crowd, but I think for the wrong reason: the constant iteration is less likely to discover underlying mechanisms than even an RCT, as it is still far too atheoretical. The link Hausmann makes to “lean manufacturing” is telling: GM famously (Henderson and Helper 2014) took photos of every square inch of their joint venture plant with NUMMI, and tried to replicate this plant in their other plants. But the underlying reason NUMMI and Toyota worked has to do with the credibility of various relational contracts, rather than the (constantly iterated) features of the shop floor. Iterating without attempting to glean the underlying mechanisms at play is not a rapid route to good policy.

（以下是私货）几个相关问题中我的回答：

• 为什么这么多人觉得社会科学中的经验研究只能建立相关性，不能建立因果性？
• DID, PSM 及 DID+PSM 有何差异？DID 要假定不可观测效应随时间变化趋势相同？

6 王同益 (实验与非实验)

社会科学研究中的“因果识别”手段可以分为两大类：实验方法和非实验方法。

对于实验方法，大家很容易想到学习生物课程时接触到的实验：一个对照组，一个实验组，两组除了我们所感兴趣的因素（记为A）不同之外，其他条件完全相同，然后我们观察到两组结果的不同就可以归结为A这个因素的影响，即A的不同就是导致结果不同的因。

社会科学研究探究“因果关系”本质上与自然科学实验所要证明的“因果关系”是一模一样的。但社会科学中涉及到的人、社会环境等等差异很大，为了使得研究结果能够推广应用到更大的群体、社会中，实验的样本就需要代表性，数量上也要求更大，所以进行社会实验的成本是非常高昂的。而且人具有能动性，对实验设计的能力也提出了非常高的要求。这也是为什么社会科学中的实验方法在近七八年来才有了显著的进展。

因此，长期起来，社会科学研究者使用的数据大多是调查收集的数据。由于调查对象的异质性、自选择行为等的存在，简单的按照某一个条件（记为B）将对象分成两组进行对比，是无法有效得出“因果关系”的，因为很难说两组对象的差异只有B这个条件的差异。类比于实验方法，其实就是没能为实验组找到一个非常好的对照组。

非实验方法的发展，一直是沿着“找/构造一个更好的对照组”这个方向发展的。从最简单的回归，到加更多的控制变量，到工具变量法IV/倾向性得分法PS/不连续回归法RD……然后越来越接近实验方法。

下面这张图归纳了实验方法-非实验方法。每一种方法的具体介绍，大家都维基百科一下，后者下载相应的介绍论文观摩一下吧。

7 brillbird (实验，DID，IV，RD，PSM)

这绝对是一个好问题啊，社会科学研究的最大问题，不就是难以识别因果关系么？前面四个答主的回答都很好，我也来凑个热闹，纯属抛砖引玉了。

Junyi Hou说的方法应该属于“新进展”，但肯定不是属于主流方法。如果题主是要做社会科学的实证研究，而不是做理论研究，那了解下当前主流的方法可能更实际，更有用。题主如果翻看主流的经济学、社会学期刊，里面做实证研究，特别是政策评估研究的，基本用的都是下面几个方法。

最简单的因果识别方法，当属普通最小二乘OLS。通过多元回归，控制其他变量，了解某两个变量的关系。国内经济学、社会学的实证研究，基本都是用OLS。要添花样的话，可以用GLS，非线性OLS。对于做微观应用计量的，离散选择模型也用的很多，logit, probit是各类期刊的常客。总之，OLS是最基础的，后面的其他方法，很多都是在它上面做改进。如果要刻意针对“因果识别”采取些纠正措施，那么下面几个方法是最常用的。

1. 实验。natural experiment, field experiement, lab experiment

比如，field experiment就是随机招募被试人群进入控制组和其他任务组，比较组别的实验结果。lab experiment顾名思义，就是在实验室里做的，商学院里研究组织行为的经常用这个方法。实验法的好处就是刻意控制干扰变量，但很多时候不具备可操作性，社会科学很多问题没法做实验啊。

2. Difference in Difference, DID，差分再差分

这算是因果识别里最常用的方法了吧，panel data, time series里都会用到，翻看社会科学里政策评估主题的文章，十篇是可能有一半是panel data+DID的。

3. 工具变量IV和2SLS

这也是解决内生性问题（典型的是回归方程中遗漏变量的问题，以及反向因果的问题）最常用的方法之一。 举个例子，大家都知道制度可能影响经济发展，但是如何用实证方法证明呢？有学者研究了曾经是殖民地的地区，用“殖民者的死亡率”做工具变量，研究制度和经济发展的关系。他的逻辑是：欧洲殖民者来到一个地方，如果这个地方环境好，那么殖民者就会从长计议，把本国的“先进”制度引进过来，搞好“制度建设”；但是如果殖民者来了之后，发现环境恶劣，自己先死了一大半，肯定就不想长远待着，那么他们就倾向于快速“掠夺”地区资源，而忽视“制度建设”。百年之后，“制度建设”型地区和“短期掠夺”型地区经济发展程度明显不同。那个学者把“殖民者的死亡率”和“人均GDP”一回归，发现果然殖民者死的多的地区，人均GDP就越低！为什么呢？只能是因为殖民者死亡率和制度建设有关系，而制度建设又影响了后来的经济发展。 工具变量的最大问题就是，找到一个好的工具变量太难了。工具变量需要若干假定，而这些假定是很难都成立的。比如上面的例子，有人质疑，殖民者死亡率之所以影响经济发展，是因为地理和气候原因！殖民者死的多，是因为地方不适宜人居住啊，鸟都不拉屎的地儿肯定经济发展不好啊，和制度没关系啊。于是就争起来了。。。（那篇文章还是发表在经济学TOP期刊《American Economic Review》上的，引用率超高，不过不少都是去反对他的）

4. regression discountinuity，翻译成中文叫断点回归，有模糊断点和清晰断点回归。

我看有知友解释了，很全面，我就不重复了。断点回归在经济学和社会学里面用的也很多，不过也有其局限性。比如，如果有多个混淆变量都有“中断”，那么就不容易知道，到底是什么造成了因变量取值的不同。

5. 倾向值匹配

这也是2000年之后用的很多的方法。它的思路很简单，就是找到“相似”的对照组和控制组成员，然后再进行比较。用这个方法，先预测倾向值（列出所有可能的混淆变量，用logit/probit预测混淆变量对因变量的影响概率），再用倾向值进行匹配，最后基于匹配样本进行因果系数估计。但是倾向值方法的劣势也很明显，比如我们不可能找到所有的混淆变量，比如它不能很好地解决交互作用问题等等。

最后，不同学科对于这些因果识别方法的运用频率，似乎也有不同。比如，工具变量在经济学里面用的很多，但是似乎社会学就用的少一些，其原因不仅来自研究问题的差异，也和学科间基本思维方式的差异有关。无论如何，方法是为问题服务的，方法是基于理论框架的。对于做实证研究的，自己研究领域内top期刊的论文，对自己肯定是最有借鉴意义的。

8 舒小曼 (实验法，RD, IV, 交叉滞后)

对这个问题非常感兴趣，借此机会，整理了下之前零散的笔记并搜集了一些新的资料，当做是一次复习和沉淀。

社会科学因果推断中面临的一个重要挑战就是：相关不等于因果（也被称为内生性问题）。也就是说，A与B相关，并不能说A导致B。也有可能是B导致A，或者A与B之外的第三个变量C既影响A也影响B，从而导致A与B的共同变化。有一个有趣的例子，即雪糕的销量和淹死的人呈显著正相关，即雪糕销量越高，淹死的人就越多。但我们不能断言说雪糕销量导致人们被淹死。事实上，这是由于二者都发生在夏天造成的。解决这一问题的方法有很多，大致可以分为两种类型，一种是从数据收集出发，通过一定的研究程序来进行因果推断，如实验法，但社会科学中的很多主题和领域没法使用实验法，这就引出了第二种类型：从数据分析出发，通过一定的统计方法来推断因果（主要针对调查数据）。

8.1 实验法（experimental method）

实验法是社会科学尤其是心理学研究中进行因果推断的重要方法。大部分心理学研究都会选择实验法，因为它能帮助研究得出因果结论。在心理学研究中，实验法甚至被称作解释因果关系的唯一方法。在这种方法中，研究者会将实验参与者随机分配到不同情境中（通常是一个实验组和一个控制组），并确保这些情境除了自变量（研究者认为会对人们的行为产生影响的变量）之外，其他的条件完全一致。这样，我们就有理由相信，不同情境下因变量的差异是由自变量造成的。 为了更为直观地理解，这里介绍一个社会心理学当中的经典实验：最简群体范式(tajfel et al., 1971; billing & tajfel, 1973)。在tajfel的实验里，实验参与者是被随机分配到两个不同的群体中（随机分配是控制混淆变量的重要手段，即保证不同情境下除了自变量之外其他条件完全一致）。在一个实验中划分的依据是他们声称的艺术偏好：Klee的画和Kandinsky的画，更喜欢哪个？在另一个实验中，通过投硬币来把实验参与者划分到两个群体中。每组成员实际上从没有见过彼此，也没有见过对方组的成员，所以两组里的人都不认识，没有任何形成内群体或外群体刻板印象的基础，这也是“最简群体”这一名称的由来。最后，tajfel和他的同事让群体成员在内群体和外群体间分配奖励（最多15分）。结果发现，分给自己组的明显多于对方组的。这被称为“最简群体范式”。

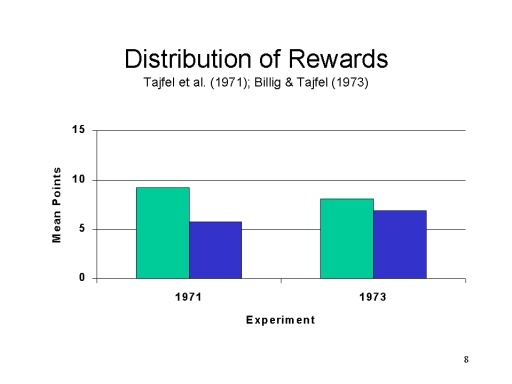
8.2 交叉滞后相关（cross-lagged-panel correlation）

先上图。

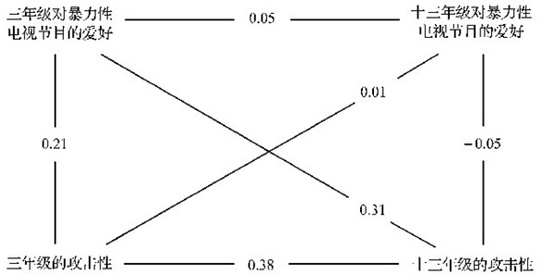
埃龙及其同事(Eron, et al．, 1972)在一项对同一组儿童进行了为期十年的追踪研究中使用了该方法。上图简要地说明了他们的研究结果。在十三年级的学生中，对暴力性电视节目的爱好与攻击性之间的相关系数基本接近于零（r=-0,05）。同样，他们也发现，三年级与十三年级对暴力性电视节目的爱好之间的相关（r=+0.05）可忽略不计。但他们在两个年级的攻击性上却获得了中等程度的相关（r=+0.38）,这说明攻击性是一种相对稳定的特质。在评估因果关系的方向时，最有趣的发现就是交叉—滞后相关（即图中沿对角线所表示的两个变量间的相关）。如果我们要问，到底是有攻击性特质的人喜欢观看暴力性电视节目还是观看暴力性电视节目导致了攻击性呢？在这种方法中，只要通过检查对角线相关，就可以确定哪一种假设更适宜。三年级的攻击性与十三年级对暴力性电视节目的爱好之间基本上没有关系（r=+0.01）。然而，三年级对暴力性电视节目爱好与十三年级的攻击性之间却存在着相当显著的相关（r=+0.31）。事实上，与早期被试在三年级时对同样两个变量所进行的研究相比，这一相关系数要大得多。因此，因果关系的方向看起来似乎是，三年级时喜欢看暴力性电视节目导致了后来的攻击行为。

8.3 断点回归（Regression Discontinuity,RD）

基本的断点回归设计是一种前测后测的两组设计。前测后测是指在处理前后施以同样的测量（实际上RD设计并不要求前后测的测量一致）。然后，我们将根据前测的断点值分配不同的人或与处理相关的其他分析单位（如家庭、学校、医院、国家）到不同的组。两组是指处理组和控制组或两个不同处理组。为便于直观理解，图示如下：

C代表根据前测断点分数分配的不同组；O代表前测；X表示实验处理或干预；上行代表实验组，下行是控制组。 慢！听起来怎么有点像实验法。断点回归与实验法的区别在于分配被试的方式不同：断点回归是根据前测的断点值（cutoff value）来分配被试的，而实验法是随机分配的。

接下来进入具体实例。假设有一个研究想要检验一种新的治疗方案对住院病人的有效性。假设有一种健康诊断，从1到100赋值，分数越高，健康程度越高。然后，我们以50分为分配标准，小于50分的人施以新的治疗方案，大于等于50分的人施以常规治疗。 下图描述了假设所有人都没有接受新的治疗方案的前后测的双变量分布。蓝X表示断点左侧的个案，他们在前后测中都是病的最严重的人。绿O代表相对来说更为健康的比较组，他们在前后测的表现都比较好。穿过双变量分布的实线是回归线，显示出前后测有很高的线性相关。

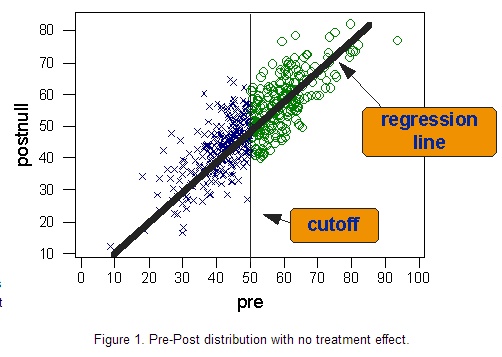
现在让我们想象实验组（断点值以下的个案）施以新治疗方案且存在积极影响的结果。为简单起见，我们假设新治疗方案对所有人的效果是一样的，都将提高10分的健康分数。如下图：

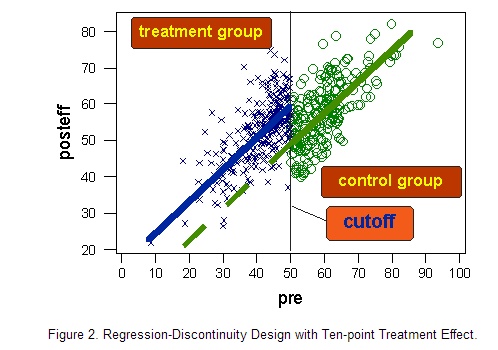
移去所有数据点，仅留下回归线，得到下图：

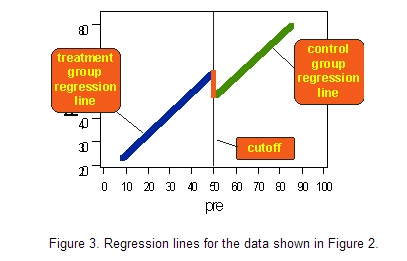
观察图3，我们很容易想到断点回归这一名字的由来。如果有治疗效果，我们会在断点附近观察到回归线的“跳跃”或“不连续”：

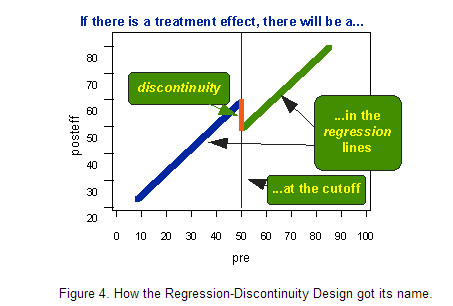
8.4 工具变量（instrumental variable）

工具变量是社会科学中基于调查数据进行因果推断的一种前沿方法。社会科学因果推断中面临的一个挑战就是：内生性问题（endogeneity）。也就是说，某个潜在的、无法观测的干扰项既影响因又影响果，导致无法做出因果推断（相关不等于因果）。例如，我们想研究家庭中的孩子数是否会影响母亲的就业，但由于生育孩子数量是可以选择的，因此解释变量存在内生性问题。工具变量就是解决上述内生性问题的重要手段。工具变量的原理最早是由Philip G. Wright在上世纪20年代末提出的。首先，我们给出一个典型的线性回归模型：

\[ y=\beta_0+\beta_1x_1+\pmb{\beta}X+\varepsilon\tag{1} \]

\(x_1\)是自变量，或者解释变量，即因，\(y\)是因变量，即果。大写的\(X\)是外生控制变量。\(\varepsilon\)是误差项。如果有一个重要变量\(x_2\)被模型(1)忽略了，且\(x_1\)和\(x_2\)相关，那么对\(\beta_1\)的估计就是有偏估计。此时，被称作内生的解释变量，也即前面所说的内生性问题。要解决内生性问题，我们需要引入更多信息。工具变量的方法引入了一个外生变量\(Z\)，且\(Z\)必须满足以下两个条件：与\(\varepsilon\)不相关，但与\(x_1\)相关。或者说，\(Z\)仅仅通过影响\(x_1\)来影响\(y\)。即：

\[\text{Cov}(Z,x_1)\neq 0;\quad =text{Cov}(Z,\varepsilon)=0\tag{2}\]

由方程(1)可以推导出：

\[\text{Cov}(Z,y)=\beta_1\text{Cov}(Z,x_1)+\beta\text{Cov}(Z,X)+\text{Cov}(Z,\varepsilon)\]

在根据方程(2)和X是外生控制变量的假设，可以得到：

\[\text{Cov}(Z,y)=\beta_1\text{Cov}(Z,x_1),\quad \beta_1=\text{Cov}(Z,y)/\text{Cov}(Z,x_1)\]

进而对进行无偏估计：

\[\hat{\beta}_1=\frac{\sum^n_{i=1}(Z_i-\bar{Z}(y_{i}-y)}{\sum^n_{i=1}(Z_i-\bar{Z}(x_{1i}-x_1)}\tag{3}\]

方程(3)里的\(B_1\)就是引入工具变量后的无偏估计量。

谈完数学模型，再来谈工具变量的基本思想。工具变量\(Z\)在模型外，是完全外生的，其只能通过影响自变量\(x_1\)而间接影响因变量\(y\)。如果\(Z\)和自变量\(x_1\)密切相关，那么，只要\(Z\)有了变化，就必然会对自变量\(x_1\)产生来自模型外的影响。如果自变量\(x_1\)和因变量\(y\)之间真的存在因果关系，那么\(Z\)对\(x_1\)的影响也必然会传递到因变量\(y\)。最终，如果\(Z\)对\(y\)的间接影响能够被统计证明是显著的，那么我们就可以推断出自变量对因变量\(y\)存在因果关系。附上陈云松老师在其论文中的图示：

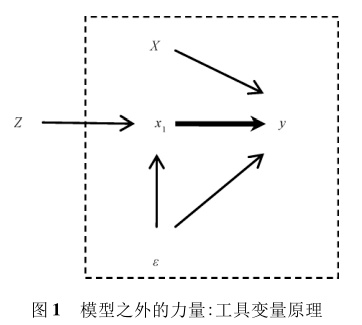
回到孩子数量影响母亲就业的例子。为了解决内生性问题，研究者巧妙地挖掘了人类生育行为中偏好有儿有女的特征，将子女老大和老二的性别组合作为工具变量。理由是：头两胎如果是双子或双女，那么生育第三胎的可能性大大增加，进而增加子女数。而子女性别是完全随机的，与母亲就业没有任何关系。

为了加深理解，这里再谈谈之前关注到的《Science》上的一篇心理学论文。弗吉尼亚大学的Thahelm及其合作者假设，中国南北方不同农作物的种植（水稻和小麦）会影响区域间的文化差异。简单来讲，水稻种植在灌溉和劳动力方面需要更多的协调和合作，因此相比种植小麦的北方，人们会表现出更多的集体主义倾向。通过调查统计发现，“水稻假说”能够很好地拟合研究中的数据。但我们不能说水稻假说就是导致南北方文化差异的原因，因为南北方除了种植作物不同外，还存在许多其他差异。为了进行因果推断，研究者使用了工具变量法。也就是说，研究者要找到一个变量，这一变量只能够通过影响自变量“种植水稻/小麦”的概率来影响南北方文化差异，而与其他不可观测的影响文化的因素无关（与误差项无关）。研究者找到的工具变量是“当地环境是否适宜种植水稻”，理由是：这一变量是自然环境决定的，不可以认为选择，是随机的、外生的。当然，这一变量是否只能通过影响农作物种植来影响文化还存在一定的疑问，但不在这里的讨论范围内。

参考文献：

1. The Regression-Discontinuity Design
2. 逻辑、想象和诠释: 工具变量在社会科学因果推断中的应用
3. 政见：“南稻北麦”真的导致了文化差异吗？
4. Talhelm, T., Zhang, X., Oishi, S., Shimin, C., Duan, D., Lan, X.,; Kitayama, S. (2014). Large-Scale Psychological Differences Within China Explained by Rice Versus Wheat Agriculture. Science, 344(6184), 603-608.

9 知乎用户

大概看了下，大多数回答不是太过繁琐就是华而不实没有直指核心，其实我觉得这类问题我看过最好的回答是 Charles F.Manski 的那篇identification problem in social sciences and everyday life，文章很短才12页，静下心来看一看会比看知乎的回答有用的多，当然我想我的这个回答应该也不会有人注意到。

10 知乎用户 (PSM)

在社会学领域，目前实证研究比较火的主要因果识别理论就是倾向值匹配（PSM，propensity score matching）方法吧，按照Morgan & Winship（2007）书中归纳，“倾向值匹配”方法广义来看包括IV啊，DID，断点回归什么的～

据说这个在国外已经火了十几年，搜causal effect能搜到好多论文把，统计系啊，经济系啊，社会学系什么的都有人在做。。。最近才在国内开始火起来……胡安宁（2012）写过一篇倾向值匹配方法的研究综述；他本人2014年发表的一篇文章也应用了该方法（广义倾向值匹配）去修正教育的回报，参见胡安宁（2014）。陈云松（2012）发表的《农民工收入与村庄网络：基于多重模型识别策略的因果效应分析》讨论了社会网络对农民工工资是否产生影响的问题；张春泥和谢宇（2013）发表的《同乡的力量》也适用了多种倾向值匹配的方法去估计network对于老乡找工作的净影响；郑冰岛和吴晓刚（2013）关于“农转非”问题的研究也使用这一方法……

一般来说，社会学在因果识别的方法主要包括实验方法和准实验方法，“random experiment”是研究的黄金准则嘛（Fisher语）～可是一般很难实现纯随机的干预，因而社会学者更多使用准实验方法去估计某类干预的净影响，PSM就是其中重要一类方法。而且我本人不懂实验方法，不能妄加评论。

按照我的理解呢，倾向值理论有两派人在搞，一类是统计学家，主要从SUTVA（Stable Unit Treatment Value Assumption）假设和Random Assignment（随机分配）假设出发，认为干预不随着个体、时间、干预的前后而发生变化，这类假设太强以至于很难在社会学中直接应用；另一类是计量经济学家，他们的IV啊，DID啊，Heckman 2SLS啊什么的，这类方法实际使用的就比较多了。具体的操作主要包括两个步骤，一计算倾向值（匹配），二是计算平均干预效应（ATE，ATT之类的）。就是在匹配之前是跑一个logistic回归计算倾向值p呢，还是算一些很有趣的距离（如Mahalanobis distance）去衡量个案之间的相似程度呢。。。具体而言不同的学者根据优化／“缺失数据”填补的逻辑去做，创造了一大堆方法，如optimal matching什么的，不过本人学的很渣，没办法系统地介绍更多了。

如果题主想简单了解一下反事实框架和因果推断不妨参考谢宇（2010）《回归分析》一书p162-169；或者谢宇（2012）《社会学方法与定量研究》（第二版）中因果推论的相关章节。系统性的读物包括当今计量真神Angrist和Pischke（2008），Morgan & Winship（2007），郭申阳和弗雷泽（2012）关于倾向值匹配的书咯～其中第一本和第三本有中译本，第二本目前还没有中译本。

不过老板说得对，统计其实不能帮助我们真正意义上解决因果关系的方向问题，很多时候都没法回避来自reverse causality的批评（类似收入决定健康还是健康决定收入这样的问题），而这因果关系的识别仍然要依赖“理论”的发展。

参考文献

1. Angrist J D, Pischke J S. Mostly harmless econometrics: An empiricist’s companion[M]. Princeton university press, 2008.
2. Morgan S L, Winship C. Counterfactuals and Causal Inference: Methods and Principles for Social Research[M]. Cambridge University Press, 2007.
3. 陈云松. 农民工收入与村庄网络: 基于多重模型识别策略的因果效应分析[J]. 社会, 2012, 32(4): 68-92.
4. 胡安宁. 倾向值匹配与因果推论: 方法论述评[J]. 社会学研究, 2012, 1: 221-242.
5. 胡安宁. 教育能否让我们更健康——基于 2010 年中国综合社会调查的城乡比较分析[J]. 中国社会科学, 2014 (5): 116-130.
6. 郭申阳, 弗雷泽. 倾向值分析: 统计方法与应用[M]. 郭志刚, 巫锡炜译. 重庆大学出版社. 2012.
7. 谢宇. 回归分析[M]. 社会科学文献出版社. 2010.
8. 谢宇. 社会学方法与定量研究(第二版) [M].北京: 社会科学文献出版社. 2012.
9. 张春泥, 谢宇. 同乡的力量: 同乡聚集对农民工工资收入的影响[J]. 社会, 2013, 33(1): 113-135.
10. 郑冰岛, 吴晓刚. 户口,“农转非” 与中国城市居民中的收入不平等[J]. 社会学研究, 2013 (1): 160-181.

11 匿名用户 (因果贝叶斯网络)

因果推断有两大框架，以 Rubin 等人发展出的 Potential Outcome 模型和 Pearl 等人发展出来的以因果贝叶斯网络（一种图模型）来给因果关系建模的方法。

似乎没人提到因果贝叶斯网络方法的发展，而我最近看到了一些相关的文章，稍微介绍一下好了。

Judea Pearl 的方法基本上在 2000 年出的 Causality 一书里面已经成型了，2009 年出了第二版。当然，相关的方法还在不断发展中。最近我看到的发展有：

1. 做出了将以反事实方式定义的因果在图模型上表示的方法
2. 将缺失值问题作为因果问题进行建模

我就只知道这么多了。正在学习中。

12 全球主义者 (质性研究方法)

在因果关系研究中，除了上述定量方法之外，质性研究方法也能提供有益的工具。“过程追踪” （process tracing）法正逐渐发展为质性研究方法中用来检验一个或者一些变量对某一社会结果的影响的最有力方法。

诚然，过程追踪不可能如定量方法那样对大量案例进行检验进而得出一般性结论，但过程追踪非常有助于达成两个目标：1. 不但验证变量的因果影响，更验证该因果关系的发生机制（mechanisms/causal processes）；2. 发现新变量，改进既有理论，或创造新理论。

不知大家对过程追踪的具体应用有无兴趣？先占坑。

13 fsaom (医学)

这个问题比较有意思，我从医学的角度讨论一下。

因果关系的确定并不容易，我们一般先是从具有统计学意义的相关关系入手。两个变量具有相关关系，例如和俗套的：小朋友和小树在某一年同时测定高度，以后每日测一次高度。我们第一个观察到的现象是人长高，树也长高。这时候我们的第一个问题是：这种现象是随机的，还是非随机的？为了解答这个问题，我们首先可以观察更多的数据，通过统计学方法，明确到这种现象是有统计学意义的，即“非随机现象”。

随后就要讨论，这个现象是否存在有因果关系，这时候我们可以从：时间关系、关联强度、可重复性、分布一致性、合理性、终止效应、特异性等方面来讨论。

• 时间关系：这个很好理解，就是“因”必然要在“果”之前。
• 关联强度：是指两个现象相关，那么它的相关程度有多大，描述关联强度的有：决定系数R²， OR，RR值等
• 可重复性：就是说你认为这两者有因果关系，那么是不是每次因出现都能有果，或者每次果之前都有因，是否可以重复。
• 分布一致性：是指“因”的分布和“果”的分布是否一致，例如说A地吸烟率高，那么A地的肺癌发生率是否也高，两者分布是否一致。
• 合理性：是指这种因果在科学上能否得到合理的解释，例如抽烟导致肺癌发生的机制已经很明确，那这就是抽烟导致肺癌的合理性。
• 终止效应：到“因”被终止后，果是不是会消失或减少。例如戒烟能降低肺癌发病率。
• 特异性：这个不太好说，现在好像也都不怎么提，我要不太懂，看有没有大神能帮我解惑一下。

因果关系的确定的确不容易，如果大家都能认识到“相关关系”不等以“因果关系”我敢保证微信微博上的那些什么“7岁男孩每天和饮料致白血病”这类的新闻会少很多。

14 知乎用户 (合成控制、同群效应、异质处理效应)

补充几个还没有提到过的进展。回头能想起来的话再补充一些简介。

15 知乎用户 (书)

推荐一本书：Morgan, S.L., Handbook of Causal Analysis for Social Research. 2013: Springer Netherlands.

16 WENN (两本书，概念与实例)

推荐两本书，基本上梳理了因果推断在社会科学的发展脉络。前一本重在概念，后一本重在实例。

• Morgan, Stephen L., and Christopher Winship. 2015. Counterfactuals and Causal Inference. Methods and Principles for Social Research. 2nd ed. Cambridge: Cambridge University Press.
• Dunning, Thad. 2012. Natural Experiments in the Social Sciences. A Design-Based Approach. Cambridge: Cambridge University Press.

关键在处理混杂因素（Confounder），粗略理了一下方法，再附上一些实例：

1. 实验 Experiment

投资对地区经济发展的影响。随机选择一些地区投资，剩下地区不投资，观察各自经济增长。

不过社会科学做实验的机会比较少，大多数还是通过观察研究。

2. 配对 Matching

研究联合国的介入对和平的影响。19组两两配对的国家，除了一个联合国介入，一个没有，其他情况综合起来（倾向得分）都差不多，比如上次战争持续时间，人口，民族结构，军队大小，民主情况，地理。

3. 回归 Regression

这个很多了，配合其他方法，但是要警惕混杂因素和内生性问题。

4. 面板 Panel

这里也包括横截面数据和时间序列数据的研究，三者的关键都在处理内生性（误差项和自变量相关）问题，涉及到的方法有Difference-in-difference model, First difference model, Fixed effects model, 基本思想是通过差分消除部分误差项的干扰。

一个例子：婚姻对男性收入的影响。一些因素会同时影响婚姻和收入，有些和时间有关，比如年龄，社会经济形势，有些和空间有关，比如地区、家庭，当然还有其他个人因素。通过差分尽量减少与时间和空间有关的误差项的干扰（如，同年龄的人比，结果就不受年龄的干扰）。

5. 断点回归 Regression discontinuity design, RDD

研究奖学金对毕业后收入的影响。假设入学考试成绩过了50分就拿奖学金，学生毕业工作后，比较那些当年拿奖学金和没拿的人的收入差距。问题是，当年考1分和考100分的人，其收入差距可能还来自本身的进取心、智力、家庭等，所以不能直接比较。所以只考虑48到52分的学生，他们其他情况差不多（没有了混杂因素），拿不拿奖学金可能是出于运气，可以看做随机的。

RDD又有精确（Sharp RDD）和模糊(Fuzzy RDD)，上面的例子是Sharp RDD。如果是Fuzzy RDD，则考试成绩越高，越有可能拿奖学金，之间是一个概率关系。

6. 工具变量 Instrument Variable

一些特殊的“随机的”变量：天气、抽签、生日

当年英国管理印度各省有两种方式，一是直接管理，建立殖民政府，收税，二是间接管理，王国自治，代其收税。我们想知道，哪种管理更有利于经济发展。初期研究表明直接管理效果更好，后来有人反对，因为直接管理的地区本来资源更丰富，农业更发达。1848至1856年一条新法令实施，只有地区国王死亡且无继承人时，英国才可直接管理该地区。这样，国王死亡作为工具变量，就可以研究管理方式对经济发展的影响。

但是，不服从指派（Non-compliance）者会出现一些问题。一个例子：服兵役对之后收入的影响。越战时期美国用抽签的方式确定服兵役资格，那么，我们可以直接比较当年服役和没有服役的人现在的收入、健康、政治观点吗？不行。虽然“抽签”作为工具变量确实随机化了，但是抽到“服兵役资格”的人最后不一定真的去服役了，可能体检不合格，可能为了推迟服役去上了大学，也有一些没有抽到服役资格的人自愿服役，这些对收入都会有影响。所以只研究有资格且服役和没资格且不服役的人（服从者Compliers）。

7. 因果图和因果机理

另外，因果图（Causal Graph）可以帮助描述变量间的关系，找到混杂因子（Confounder）、中间变量（Mediator）、冲撞点（Collider），无法观测的变量等，再考虑用上述方法处理混杂因素，方便又直观。推荐工具：DAGitty

其次，一些研究重新回到了探索因果机理（Causal mechanism），而不只局限于研究因果效应（Causal effect）的存在和大小。举个例子，假设，恐袭新闻导致当地民众反对外来移民，我们想要知道这个假设是不是对的，程度大不大，同时，我们也想知道这中间的原理是什么，新闻导致恐慌进而导致反对情绪，还是新闻导致反恐开支增加进而导致反对情绪。重点在分解直接因果和间接因果，间接因果即假设的机理，然而传统方法中介研究Causal mediation analysis(Barron, Kenny 1986)有可能因为受到无法观测变量的干扰，得出错误的结论。近年序列可忽略假设（Sequential ignorability assumption）提出后，再加上Pearl的图，因果分解变得容易不少。

17 知也 (严辰松-定量型社会科学研究方法)

因果关系成立的三条件：怎样判断事物间有因果关系？一般认为，两事物间因果关系成立的条件是：（1）从发生顺序上，因在前，果在后（temporal order）；（2）它们之间有关联（association）或者说共变（co-variation）的关系；（3）必须排除其他可能用于解释结果的因素（elimination of spuriousness)。现分别来说明。

先说时间顺序。假如我们认为两事物之间存在因果关系，而现在需要确定孰是因，孰是果。直觉告诉我们，只有发生在先的事物才可能是因，时光倒逆只是幻想。时间先后顺序说不清而无法断定孰是因孰是果的，两者有可能互为因果。如贫困与多生多育的关系。多生多育也许是贫困的原因，然而后者未尝不是前者的原因。因为穷，所以想多生一些孩子以增加劳力、摆脱困境。

时间顺序是因果关系的必要条件，但并非充分条件。把凡是发生在先的就作为因，显然大谬不然。如我在屋子里打了个喷嚏，外面紧跟着就响了个雷。能说我的喷嚏引起了打雷吗？不能。有个老师骑车摔骨折了，一查原来是家里前一天未给供奉的菩萨烧香。这未免荒谬。尽管如此，仍然有不少人错把时间顺序当作因果关系唯一的条件。

再说关联。关联就是通常所说的“相关性”（co-relation）。当自变量引起因变量的变化时，两个变量之间有一种恒定的联系，也就是说，自变量方面的每一个变化都引起因变量相应的、可以预见的变化。如果研究表明，每当我们改变事物的一个方面，事物的另一个方面就出现可以预见的变化时，我们就会考虑前者是否导致了后者。假设我们在不同的情景和条件下，重复同一个实验，这种共变关系总是保持不变，我们对当初的判断就更有信心了。

两事物之间的共变关系有方向和强度的问题。当自变量的值上升、因变量的值也相应上升时，两者呈正向的联系；而当前者上升、后者下降时，两者呈负向的联系。联系的强度说明共变的显著性。方向和强度都可用统计学中的相关系数来表示，可用统计软件进行计算。相关系数数值的范围是-1至+1之间，越向两端，强度越大；正号表示正向的联系，负号表明是负向的联系，零表示没有联系。

必须注意，两事物之间的共变关系并非一定是因果关系。许多共变的事物之间并无因果关系。有人说，他家不能喝椰子汁，一喝椰子汁就出事，如丢东西，孩子生病等，因此家中现在决不喝椰子汁。这未免可笑。在很多时候，有高度相关的两件事情其实风马牛不相及。比如，美国婴儿腹泻发病率与南部各州柏油路路面的粘滞度呈高度相关。再比如，在上世纪60和70年代，印度儿童的出生率和美国人使用美国造汽车的比率呈高度相关。

像时间顺序一样，共变关系是因果关系的必要条件，但却也不是充分条件。必要条件，顾名思义，指的是事件发生必须具备的条件。如，必须是成熟的女性才能怀孕。然而仅仅是成熟的女性并不就能怀孕。怀孕还需要一个充分条件。充分条件是可以有的条件，而且，一旦具备这个条件，事件就必然会发生。显然，怀孕的充分条件是交媾和受精，这是产生胚胎的充分条件。再比如，给孩子喂奶是孩子生长的充分条件，因为只要有奶喝，孩子必然能发育长大。但是喂奶并不是生长的必要条件，因为喂别的食品，孩子也能获得生长需要的营养。因此，假如我们寻找促使孩子生长的根本原因或唯一的原因，喂奶肯定不是，因为它不具备双重身份，即既是必要条件又是充分条件。当且仅当一个事物既是另一事物发生的必要条件又是充分条件的时候，前者才是后者的真正的原因，即唯一的原因。

确立因果关系的第三个要求是尽可能排除其他可用于解释结果的因素，也就是排除干扰变量（confounding variables或confounds）。歇洛克·福尔摩斯破案是根据证据进行推理。是男管家干的吗？不像。不可能是男管家干的，因为床上的头发是金色的，而管家的头发是黑色的。然而管家会不会有意将金色头发放在那儿迷惑大家呢？科学工作者就像侦探，要确定导致研究（如实验）结果的是否还有其他原因。面对已有的信息，研究者不断思考这样的问题：我们能做出什么样的推论？推论合理吗？逻辑是回答这些问题的有力武器。研究者必须通过精心的设计，审慎的操作，竭力排除对研究结果其他可能的解释，使人信服拟议中的因果关系不是假象（non-spurious)。

值得注意的是，不管怎样努力，在社会科学研究中，我们所说的因果关系中的因，一般都不是那种唯一的原因，即既是后面结果的必要条件又是充分条件。我们只是说，两个事物之间在很多情况下，具有系统的联系。

有些哲学家干脆认为，因果关系是研究者赋予情景的，只表示研究者对世界的认识，并不一定反映现实本身。我们做出的只是对世界的推论，不能说我们已经发现了真实的世界。尽管如此，社会科学家和自然科学家一样，他们孜孜以求的目标仍然是寻找或确立事物间的因果联系。

与其他任何研究方法相比，实验研究最适宜用来验证事物间的因果关系。因果关系的三项条件，时间顺序，关联和排除其他可能的解释，都能在实验研究中得到清楚的论证。

（摘自严辰松《定量型社会科学研究方法》第八章）

18 HiI’mPsycho (心理学中的三个条件)

心理学里面要make a causal claim必须要满足三个条件: temporal precedence(一个变量先改变); covariance(两个变量相关); internal validity(没有其他第三变量或者替代解释)。最简单的方法就是做实验，因为你可以控制变量。也可以做quasi-experiment(准实验)，但会牺牲一些internal validity;也可以做case study，但是generalizability不够。(自己的取舍就比较重要了)

还可以做很多longitudinal和相关，然后找最简的解释。当然心理学属不属于社会科学要另外考虑了(物理学、数学:“必须是！”

19 张序 (流行病学专业)

因果识别方法不请流行病学专业，答主很生气。

在流行病学专业当中，因果识别是非常困难的，所以当你选择流行病学课的时候，因果判断可能被当做非常重要的一个章节去讲。

1. 因果关系的判定极为困难

如今，因果判断有了很多的发展，上学的时候学了很多的准则，mill方法，hill策略。。但是最终发现，无论怎么证明，因果总是有点证不明。 所以我们很多人开始使用循证医学的方法，综合样本，然后用不同的证据去证明。 而你的理论假设证明了，那现实当中如此众多的混杂依旧没有排除。所以，当我们要想找到因果关系的时候，总是那么困难。

2. 因果关系在不断被证明-推翻-再证明的过程

在流行病学研究中，其实有很多研究基于社会因素，而也正是这些因素，是最难以研究的，经常看到，不断的有新的同行进入，在原有的假说上继续证明，很可能就是因为别人认为，可能某个因子可能是一个混杂因素。要知道，当有可能有混杂因素存在的时候，因果可能偏差的非常大。比如说，我们开脑洞的研究穿短裤与雪糕销售的关系，然后发现有统计学关联，但是这样的关联是因果吗？当然不是的，这个关联仅仅是一个统计学关联，也就是数学上看起来有意义，实际上不是真正的因果联系，而真正的因果，大家都知道，其实是因为夏天温度高，所以冰棍卖的快，而这样的假关联在统计上我们只要一排除，马上可能发现没有关系。

当然也可能甚至变高了，因为在调查过程中，还有各种各样的问题，可能由于你的设问方式不对，又出了新的结果。

所以这么诸多的问题，在证明一个假设的时候不同的学者都要争论很多年，就一个吸烟和肺癌，从一开始的没有关系，到确定是独立危险因素，用了好几十年，在不断推翻重建当中，找到的证据质量都在升级。

3. 常用方法

当然啦，横断面，病例对照。也都可以证明因果关系当中的部分。

但是如果说，真的要想证明因果关系，无论什么学科，都只有两种方法，就是队列研究，还有实验。因为，其他的一切的找到关联的研究模式，都不能解释关联的时序性。我们看看统计就知道，既是是纵断面的时间序列，也不能够一边解决关联强度，还有关联时序性的问题。

统计只是告诉我们关联。

我们只有跟踪一群人，无论干预与否，然后采集结果，这样研究才有时序性可言。但是，当然这个开销巨大，花费的资金可能近乎天量资金，然后不一定能够得到我们想要的数据。

20 因缘际会 (方法论文章推荐)

若对最近十年内关于因果关系提取的进展感兴趣，或许可以看下面这篇文章的第二部分：Causal discovery and inference: concepts and recent methodological advances。最近十年内这个领域有很大的发展。具体来说，两个IID的变量之间的瞬时因果关系一般也都能从被动观测数据中提取出来。而且因果关系在machine learning里面有直接用途。

21 知乎用户 (空话)

好有意思，因果识别竟然什么学科都抛出来，因果识别就是建立一个逻辑关系。无非就是在所有事物中找出与目标相关联的因素，因素中存在直接发生效用的就是因果。 这东西国外论文不可能说清楚，看汉语或汉字，根据汉语的词性来归类是最简单的方法。如果你想问的是统计概率或是量化中的要素关联权重的识别问题，那个不属于因果，属于归纳汇总的逻辑方向。

因果有几个基本的特征，第一个，单一要素构成，既一个原因匹配一个结果，多个因素构成一个结局是统计，一个事物包含多少个要素是量化，是否发生判断发生等是概率，单纯的因果只有1对1，不能有两个原因导致1个结果。人类社会行为全部是从结果去找原因，而并非是找寻结果答案。

如某日某地发现一尸体，这是最现实的状况，这里只有结果没有原因，结果是人死了，然后叠加要素来判断原因，自杀还是他杀，这个是最简单的因果状态，一个结果由一个原因所致，死是一个状态的表现，所以一般具有状态表述性的词语都具有结果性质。 那么不可能没有原因的死掉一个人，就算是猝死那也得是在患有相关疾病的情况下。所以怎么死的就是死的原因，这个是核心逻辑，如果是被杀，那么被谁杀和动机就属于引发核心的本质逻辑的原因逻辑，也就是一件事物是在核心的本质逻辑之上又叠加了其他的逻辑所组合成的整体而切均为必然性质。

凡是带有主观目地性的词语大都具备原因要素，动词居多，像生活中最长碰到的语言逻辑会出现这种问题，你你又没喝酒为什么去厕所？去厕所是对结果的一种表述，就以小便来说，问题就不是建立在同一逻辑关系上，小便是因为尿急而不是因为喝酒，喝水也会尿急，而尿急的原因也不是喝酒或喝水，酒水只是说明，跟厕所的用意一样，原因是你喝了。所以喝东西到去小便是两层逻辑，而如果是去厕所又包含了对小便的说明，又含有逻辑。以上是比较基础的逻辑因果关系。

难点的如有效关心 1+1=2 这种逻辑就比较难做因果。总的来说现代科学基本是以数学的方式在不动的角度对不同的因果做解读从而能够建立逻辑