你的选择是？Roy 自选择模型及前苏联的数学家们（Labor系列） - 慧航 - 专栏

原文地址：https://zhuanlan.zhihu.com/p/20009505

前苏联解体后有将近 300 多位苏联数学家移民到了美国。经济学家们当然没有放过这么好的研究机会（而且是对数学家评头论足的机会），于是有了哈佛肯尼迪政治学院 George Borjas 和诺特丹大学 Kirk Doran 2012 在 Quarterly Journal of Economics 发表的《苏联解体对于美国数学家的影响》The collapse of the Soviet Union and the productivity of American mathematicians。

激发 Borjas 写这篇文章的可能是他对 Roy 自选择的理解。最早提出自选择概念的是英国经济学家 A.D.Roy。他于 1951 在 Oxford Economics Paper 发表了题为《针对收入分配的一些想法》Some Thoughts on the Distribution of Earnings 的论文。文章讨论了为什么不同职业的收入是不一样的。Roy 最重要的想法是，我们不能假设每种职业的收入都完全由外因决定， 在自由就业的情况下，人们会根据自身偏好和特长作出不同的选择。这种自我选择行为于是被称为 Roy 自选择模型。也许这种想法当下看来明显不过，但过去的很长一段时间里职业并不是个人选择而定的，于是经济学家也想当然得认为职业报酬“好像是历史偶然因素造成的” －“developed by the process of historical accident”。但对于现在很多 Labor Economics 问题，自选择模型都非常有用。其中 George Borjas 于 1987 发表的Self-selection and the earnings of immigrants最为经典（原文在 American Economic Review 上，推荐一读。）他用 Roy 模型来分析移民这种二元选择 。曾经人们普遍认为移民只对于高收入工种有促进作用，但鉴于这几年美国共和党和民主党对于非法移民改革争议连连，我们也知道移民对于低收入工种也是意义深远的。Borjas 对 Roy 模型的应用能很好的解释高收入移民和低收入移民（还有第三种不常发生的政治移民。）我们先来看一下 Borjas 对 Roy 模型的提炼（其实模型可以简单概括为人往高处走，水往低处流。不知各位看法如何？）

以下我们标记本国为 country 0，移民国为 country 1。首先假设收入在国家\(j\)可以表达为\(\ln w_{j} = \mu_j + \epsilon_{j}\)。同时标记协方差为\(\sigma_{0,1}= cov(\epsilon_{0},\epsilon_{1})\)。假设\(\epsilon_{0}\)和\(\epsilon_{1}\)是联合正态分布，也就是说

\[\left(\begin{smallmatrix} \epsilon_{0} \\ \epsilon_{1} \end{smallmatrix} \right) \sim N \left( \left( \begin{smallmatrix} 0 \\ 0 \end{smallmatrix} \right), \left(\begin{smallmatrix} \sigma_0^2 & \sigma_{0,1} \\ \sigma_{0,1} & \sigma_1^2 \end{smallmatrix} \right) \right)\]

这里关于收入的假设是：一部分收入由 observable characteristics 可观察特征决定，如教育水平(\(\mu_0\)和\(\mu_1\))；另一部分则由不可观察特征决定 unobserved characteristics (\(\epsilon_{0}\)和\(\epsilon_{1}\))。

标记\(\rho_{0,1}\)为\(\epsilon_{0}\)和\(\epsilon_{1}\)的相关系数，那么

\[\rho_{0,1}=\frac{\mathrm{cov}(\epsilon_0,\epsilon_1)}{\sigma_0 \sigma_1} = \frac{\sigma_{0,1}}{\sigma_0 \sigma_1}\]

假定移民的开支\(C\)是在本国收入的一部分，即\(C = \pi w_0\)，这样后面我们可以简化¹\(\ln(w_0 + C) \approx \ln(w_o) + \pi\)。

接下来我们便能导出移民决策啦。即根据以下\(I\)的正负来决定。正的时候移民后的收入更高，会选择移民；反之则留在本国，即

\[ \begin{aligned} I = \ln \left( \frac{w_1}{w_0 + C} \right) &= \ln(w_1) - \ln(w_0(1 + \pi)) \\ & \approx (\mu_1 - \mu_0 - \pi) + (\epsilon_1 - \epsilon_0) \end{aligned} \]

接着标记\(v \equiv \epsilon_1 - \epsilon_0\)，我们知道\(v\sim N(0, \sigma_0^2+ \sigma_1^2-2\sigma_{0,1})\)。这样的话一个人准备移民的可能性可以写作

\[ \begin{aligned} \mathrm{Pr}(I>0) & =\mathrm{Pr} [ \epsilon_1 - \epsilon_0 > - (\mu_1 - \mu_0 - \pi)] \\ & = \mathrm{Pr} [v > - (\mu_1 - \mu_0 - \pi)] \\ & = \mathrm{Pr} \left[ \frac{v}{\sigma_v} > \frac{\mu_0 - \mu_1 + \pi}{\sigma_v} \right]\\ & = 1 - \mathrm{Pr} \left[ \frac{v}{\sigma_v} \le \frac{\mu_0 - \mu_1 + \pi}{\sigma_v} \right]\\ & = 1 - \Phi \left( \frac{\mu_0 - \mu_1 + \pi}{\sigma_v} \right) \\ & = 1 - \Phi(z) \end{aligned} \]

其中我们标记\(z = \frac{\mu_0 - \mu_1 + \pi}{\sigma_v}\)。如果\(z\)值更高，那么就越不可能移民，影响\(z\)值的有本国收入，移民国收入，移民所需费用和\(z\)的标准差。前面三项都是比较直观的因素，接下来我们更多的探讨这个标准差的影响。

对于已经准备移民的人，我们也想知道他们在本国是处于什么样的收入情况，是高收入还是低收入，即\(\mathrm{E}(\ln w_0 | I > 0)\) 和 \(\mathrm{E}(\ln w_1 | I > 0)\)相对本国平均收入的大小。相关推导可以查看原文，以下我们直接看自选择结果啦。

假设两国的平均收入相等，那么对于移民的人们，比较他们在本国和在移民国的收入分布主要看\(Q_0\)和\(Q_1\)的正负：

\[ \left\{ \begin{aligned} Q_0 \equiv \mathrm{E}(\epsilon_0|I>0) &= \frac{\sigma_0 \sigma_1}{\sigma_v} \left(\rho_{0,1} - \frac{\sigma_0}{\sigma_1} \right) \left( \frac{\phi(z)}{1-\Phi(z)}\right) \\ Q_1 \equiv \mathrm{E}(\epsilon_1|I>0) &= \frac{\sigma_0 \sigma_1}{\sigma_v} \left(\frac{\sigma_1}{\sigma_0} - \rho_{0,1} \right) \left( \frac{\phi(z)}{1-\Phi(z)} \right) \end{aligned}\right. \]

有以下三种情况：

1. 正向选择移民\(Q_0>0,Q_1>0\)（\(\rho_{0,1}> \frac{\sigma_0}{\sigma_1}\)而且\(\frac{\sigma_1}{\sigma_0}>1\)），即在本国收入和移民国收入都很高，但是移民国的收入分配比本国更加分散。比如欧洲的好医生移民到美国，因为美国医生的收入相对平均收入要高很多。
2. 负向选择移民\(Q_0<0,Q_1<0\)（\(\rho_{0,1}> \frac{\sigma_1}{\sigma_0}\)而且\(\frac{\sigma_0}{\sigma_1}>1\)），即在本国收入和移民国收入都很低，但是移民国的收入分配比本国更加集中。比如墨西哥的劳工移民到美国，因为能享受更好的社会福利。
3. \(Q_0<0,Q_1>0\)（\(\rho_{0,1}<\min(\frac{\sigma_0}{\sigma_1},\frac{\sigma_1}{\sigma_0})\)）移民是负向选择，但收入在两国没有相关性。Borjas 说此类为难民式移民或曰政治性移民，比如人们逃离专制国家。

关于第一种（高收入自我正向选择）和第二种（低收入自我负向选择）都有很多研究，而第三种情况较少。但就在这篇文章发表后不久，苏联解体了，Borjas 当然没有放过这个机会。虽然搜集数学家的 panel data 很费事²，但还是有了开篇提到的这篇文章。

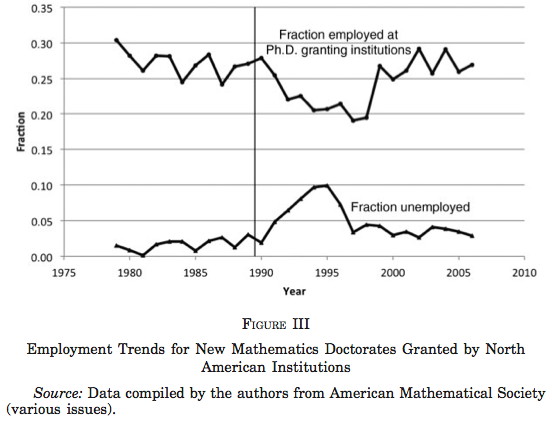
来到美国的数学家们都是同行中的佼佼者，其实也是正向选择移民。意外（不意外？）的是美国的数学家并没有因为和苏联学术交流，而提高自身水平，Borjas 和 Doran 估算苏联数学家的涌入在 1992 到 2008 间减少了美国数学家近三成的发表量，而且 1992 年左右的美国本土博士生们都就业难了。

虽然是从移民的自选择问题出发，Borjas 和 Doran 的意图更在于讨论学术人才涌入对于本国学术人才的影响。学术圈一方面是在教职上竞争，另一方面是发表论文数上竞争。当然论文发表量并非是一个好的测量方法，我们都知道钱学森归国对我国航空事业还是有巨大贡献的（如题图。）

所以想问大家对于学术圈 productivity 有什么好的测量方法吗？你觉得自选择模型还能解释哪些别的现象呢？

李一鸣：Moser, Voena, and Waldinger (2014) 用专利申请数目来探究二战期间犹太裔德国化学家到美国以后的影响。

nautilus sun：“In the second step of our data collection, we hand-match émigrés and other German chemists with U.S. patents between 1900 and 1970.” 好同情挖数据的小朋友们。不过你记得文章有看多少专利是化学家从 industry 里申的还是从 academia 里申的？

李一鸣：我没读过论文，只听 Voena 讲过一次。我记得他们搜集的专利好像是教授的专利。

Loser Loser：人们会根据自身偏好和特长作出不同的选择为什么会造成不同职业的收入是不一样的？还是没明白…

nautilus sun：假设劳工市场是 perfect competition，那么工人的 wage 等于他们的 marginal product of labor。因而 high productivity worker 选择的职业会是高收入的职业。至于为什么不同国家同一职业的收入分布会不一样，除了 productivity 不一样之外，我想还有就是社会福利政策。寻租行为也会导致非 perfect competition，例如开出租车要有营业执照。