原文地址:https://zhuanlan.zhihu.com/p/20294874
在实证中,工具变量(IV)是非常常见的识别策略,而Imbens and Angrist(1994)则提出了工具变量的一个『局部平均处理效应』(Local Average Treatment Effects,LATE)的解释。根据 LATE 的解释,在处理效应的语境下,工具变量识别的是那些因为工具变量的变动而导致项目参与会改变的子样本的平均处理效应,即 Compliers 的平均处理效应。然而 LATE 仍然是需要一些假设的,而对于这些假设是否能够满足,一般的文献里面似乎很少讨论。Damon Jones 的NBER working paper《The Economics of Exclusion Restrictions in IV Models》讨论了这其中『排除性限制』可能违反的情况,并给出了一些补救的策略。
我们先从 LATE 的一般设定开始。假设\(D_i\)为处理状态,\(y%为关注的结果,潜在的结果可以是一个处理状态\)D\(以及工具\)Z\(的函数。假设\)Z$也为\(0-1\)变量。那么 LATE 的假设可以总结为:
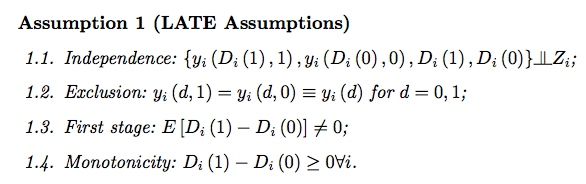
其中第一条为独立性假设;第二条为关键的『排除性限制』,即假设工具变量\(Z\)不会影响潜在的结果\(y\);第三条假设为第一阶段回归中\(Z\)对\(D\)有影响;最后一条假设为单调性假设,即这里假设了工具变量\(Z\)对\(D\)的影响是单调的。
LATE 的估计量可以写为:
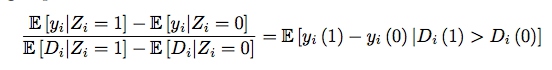
即估计的结果为那些可能因为工具变量的改变而改变自己行为的那些个体的平均处理效应。
作者认为,这其中的第三条假设在一般的效用最大化框架下是否满足需要仔细考虑。为此,作者提出了一个比较一般化的效用最大化框架。在这个模型里面,个体分两阶段最大化自己的效用,在第一阶段,个体在工具变量Z的影响下,选择是否参与项目:
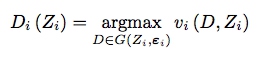
其中\(v\)为第二阶段最优化的 value function,第二阶段的最优化问题为:
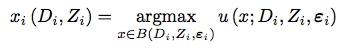
即个体通过在约束集\(B\)中选择\(x\)最大化效用函数\(u\)。这个模型是一个非常一般化的设定,比如常见的 Roy 模型也为这个模型的特例。
那么什么情况下会导致以上的『排除性限制』失效呢?作者提出,只有当个体所面临的约束集\(B\)不随工具变量Z变化,同时效用函数也不随工具变量\(Z\)变化时,『排除性限制』是满足的,即:
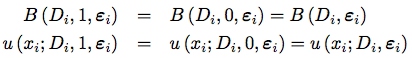
然而在某些情况下,以上条件并不满足。
作者举了一个例子。比如在研究教育回报的时候,由于上不上大学(\(D\))是由个体自己选择的。现在有一个学费减免的政策,假设这个学费的减免是随机的,因而潜在的可以成为工具变量。假设学费为\(p\),上大学会使得工资增加一个倍数\(\phi\),假设\(l\)为劳动供给,\(I\)为非劳动收入,则个体面临的问题为:
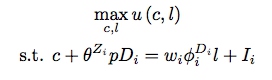
在这里,结果变量为劳动的总收入,然而问题是,对于那些总是会上大学的个体(\(D(1)=D(0)=1\)),如果接受了学费的减免,那么会对个体面临的预算约束有影响,进而对其劳动供给行为造成影响:
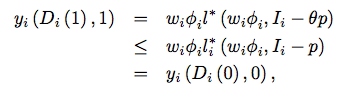
在这里,工具变量对于个体的行为产生了收入效应,因而之前的『排除性限制』假设被违背了。
那么如何解决这一问题呢?作者提出了两种方法。
第一种是可以使用文献中的结果对 LATE 的估计结果进行校准。比如在以上的例子中,作者计算出,使用 LATE 估计出的处理效应应为:
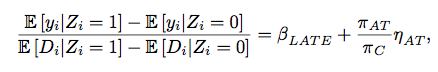
其中:
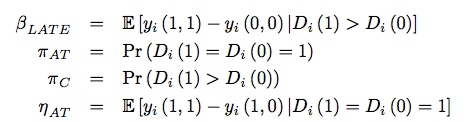
因而如果知道了最后的三个参数,就可以对以上的结果进行校准。作者引用了 Zimmerman,(2014)的 IV 估计结果 0.22,以及 Rothstein and Rouse (2011) 对\(\eta\)的估计结果,计算出由于忽略了收入效应,使得 IV 的估计结果有大约 0.1 的偏差,应为\(0.22+0.1=0.32\)。
第二种方法是,如果条件允许随机试验,那么可以增加一个随机试验来识别上式中的\(\eta\)。比如在以上的工具之外,实验设计者可以给试验对象一个额外的现金,比如\((1-\theta)p\),那么使用这个额外的工具,潜在的收入效应规模也可以被识别。
一般说来,『潜在结果』模型的支持者对结构模型的一大批评是给出的假设太多,而现实情况经常不符合这些假设。而这篇文章则使用了一个效用最大化的框架,给潜在结果模型的假设提了一个现实的问题,是一个不错的视角。
薛熠:不做劳动经济学,但为什么不直接看工资?而是看劳动总收入?如果看工资就没这个问题了。
慧航:因为问题是劳动参与啊
薛熠:我以为是教育回报,感觉 wage 就够了。