慧航

既然被邀请和提到，在这里我来写一个最简单的 GMM 快速入门手册吧，因为这个技术听起来非常的高大上，但其实非常简单。如果你有本科的统计知识，看懂下文是不成问题的。

GMM 的全名是 Generalized Method of Moments，也就是广义矩估计。只看这个名字的话，如果去掉广义这个词，可能学过本科统计的人都认识，就是矩估计。

矩估计是什么呢？简单的说，就是用样本矩代替总体矩进行统计推断的方法。一个最基础的例子是正态总体的参数估计问题。如果\(x_i\sim N(\mu,\sigma^2)\)，如何估计\(\mu\)和\(\sigma\)呢？

本科的统计学一般会介绍两种方法：极大似然估计和矩估计。其中矩估计是我们今天的主角。观察到：

\[\mathrm{E}(x_i)=\mu,\quad\mathrm{E}(x_i^2)=\mu^2+\sigma^2\]

而根据大数定理，在一定的条件下，我们有：

\[\overline{x_i}-\mu=o_p(1),\quad\overline{x^2_i}=\mu^2+\sigma^2+o_p(1)\]

也就是说，当样本量足够大的时候，样本矩与总体矩只差了一个无穷小量，那么我们是不是可以用样本矩代替总体矩得到参数的估计呢？

按照上面的思路，我们把\(o_p(1)\)去掉，同时把未知的总体参数写成其估计值，也就是带^的形式，我们得到了：

\[\hat{\mu}=\overline{x_i},\quad \hat{\sigma}^2=\overline{x^2_i}-(\overline{x_i})^2\]

如此，我们得到了两个总体矩的点估计。在这个简单的例子里面，你只要把上面的大数定理的结论带到上面两个式子里面，很容易的就可以证明出两个点估计是一致的估计量。

当然，值得注意的是，即便我使用的是矩条件，\(\sigma\)的估计也不是无偏的。一般而言，除了特殊情况，不管是 MLE 还是 MM 还是 GMM，都不一定可以得到无偏的估计量。特别是在比较复杂的应用里面，一致就很不错了，无偏性的讨论真的繁琐。

好了，上面是矩估计，非常简单是吧？但是什么又是广义矩估计呢？

在上面的例子中，我们只使用了两个矩条件。然而我们知道，正态分布的矩是有无穷多个可以用的，那么我们是不是可以使用更多的矩条件呢？

但是有个问题不好解决。在这个例子里面，我们有两个未知参数，如果只使用一阶矩，那么只有一个方程解两个未知数，显然是不可能的。像上面一样，我们用两个矩条件解两个未知数，就解出来了。然而，当我们用一到三阶矩，总共三个方程求解的时候，三个方程求解两个未知数，可能无解。

方程数多了，反而没有解了，为什么呢？其实很简单，用三个方程中的任意两个方程，都可以求出一组解，那么三个方程我们就可以求出三组解。所以应该如何把这些矩条件都用上呢？

到这里我们不妨引入一些记号。还是使用上面的例子，我们把上面的三个矩条件写到一个向量里面去，记：

\[g(x_i,\theta)=\left[ x_i-\mu, x_i^2-\mu^2-\sigma^2, x_i^3-\mu^3-3\mu\sigma^2\right]^\prime,\;\theta=\{\mu, \sigma^2\}\]

我们可以得到一个3*1的列向量，并且：

\[\mathrm{E}[g(x_i,\theta)]=0\]

上面就是我们要用的矩条件。而根据上面的思路，用其样本矩代替总体矩：

\[\begin{equation} \frac{1}{N}\sum_i g(x_i,\hat{\theta})=0 \end{equation}\]

解这个方程应该就可以得到参数\(\theta\)的估计。但是正如上面所说的，三个方程两个未知数，并不能确保这个方程有解，所以必须想一些其他办法。

一个比较自然的想法是，上面的矩条件等于\(0\)，虽然我不太可能保证三个方程同时等于\(0\)，但是仿照 OLS，我们可以让他们的平方和最小，也就是：

\[\min_{\hat{\theta}} \left[ \frac{1}{N}\sum_i g(x_i,\hat{\theta}) \right] ' \left[ \frac{1}{N}\sum_i g(x_i,\hat{\theta}) \right]\]

这样我们就能保证三个矩条件的样本矩都足够贴近于\(0\)，当然不可能同时为\(0\)。这样不就综合使用了三个矩条件的信息么？

更一般的，由于上面的\(g\)函数是一个3*1的列向量，我们可以使用一个权重矩阵\(W\)来赋予每个矩条件以不同的权重：

\[\begin{equation} \min_{\hat{\theta}} \left[ \frac{1}{N}\sum_i g(x_i,\hat{\theta}) \right] ' W \left[ \frac{1}{N}\sum_i g(x_i,\hat{\theta}) \right] \end{equation}\]

只要这个\(W\)是一个正定矩阵，那么仍然可以保证每个样本矩都足够贴近于\(0\)。

那么问题来了，既然对\(W\)的要求只要求正定矩阵，那么使用不同的权重矩阵就有可能得到不同的结果。问题是，有没有一个最优的权重矩阵呢？当然是有的。可以证明，最优的权重矩阵应该是：

\[\begin{equation} \left\{\mathrm{E} [g(x_i,\theta)g(x_i,\theta)^\prime] \right\}^{-1} \end{equation}\]

使用这个权重矩阵，就得到了最有效的估计。

比如上面的例子，用 gretl 分别估计两个矩条件、三个矩条件使用单位阵作为W、三个矩条件使用最优权重矩阵做估计：

nulldata 1000
set seed 1988
series x=randgen(N,1,2)
series x2=x^2
series x3=x^3
series e
series e2
series e3
scalar mu=0
scalar sigma2=1
matrix W2=I(2)
gmm
    series e=x-mu
    series e2=x2-sigma2-mu^2
    orthog e; const
    orthog e2; const
    weights W2
    params mu sigma2
end gmm
matrix W3=I(3)
scalar mu=0
scalar sigma2=1
gmm
    series e=x-mu
    series e2=x2-sigma2-mu^2
    series e3=x3-3*mu*sigma2-mu^3
    orthog e; const
    orthog e2; const
    orthog e3; const
    weights W3
    params mu sigma2
end gmm
scalar mu=0
scalar sigma2=1
gmm
    series e=x-mu
    series e2=x2-sigma2-mu^2
    series e3=x3-3*mu*sigma2-mu^3
    orthog e; const
    orthog e2; const
    orthog e3; const
    weights W3
    params mu sigma2
end gmm --iterate

首先是使用两个矩条件的结果：

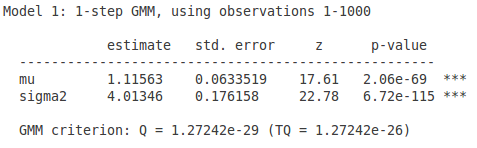
1. 为什么两个矩条件的时候不使用最优权重矩阵呢？因为两个未知参数，两个矩条件，不存在过度识别的问题，存在唯一解的，所以不管使用任何的正定矩阵，得到的结果都是一样的。

三个矩条件，这个时候使用什么样的权重矩阵就不一样了。

2. 先使用单位阵作为权重矩阵：

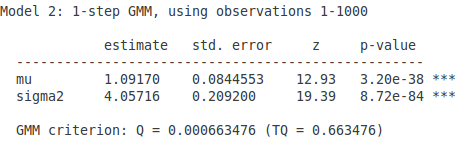
这里需要注意的是，即使使用了更多的矩条件，估计量的 standard error 还是变大了。感兴趣的可以做一个蒙特卡洛模拟试试，一定是会变大的。为什么呢？因为没有使用最优的权重矩阵，所以使用单位阵作为权重矩阵得到的结果不是最有效的。

3. 那么如果使用最优的权重矩阵呢？结果：

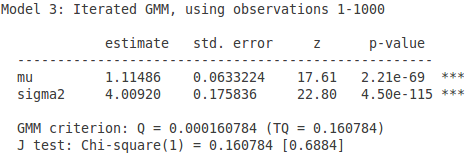
嘿！standard error 是变小了，但是跟使用两个矩条件的好像没有什么本质变化啊？为什么呢？

因为这里举的这个例子太特殊了，我们使用的前两个矩条件，刚好是一个充分统计量，也就是说，使用额外的矩条件不会带来附加信息的。但是如果是其他情况，一般来说更多的矩条件是可以带来更多的信息的，比如工具变量的回归。

另外如果细心观察，最后一张表格多了一个 J-test。这又是啥呢？

这个东西就比较有意思了。直到现在，我们都是假设使用的矩条件成立，那么这些矩条件真的是成立的么？未必啊。比如，如果\(x\)本来就不服从正态分布，那么使用上面的估计显然是错的。那么是不是可以检验矩条件是否成立呢？

一般来说，如果你有\(K\)个未知的参数，以及\(K\)个矩条件，那么矩条件是不能检验的。但是如果你有更多的矩条件，那么就有了检验的可能。这个检验的直觉很简单，比如上面的例子里面，我们有\(3\)个矩条件。我可不可以先使用前两个矩条件估计这两个参数，然后把这两个参数带入到第三个矩条件里面，看看是不是充分接近于$0$，如果充分接近，那么看来这三个矩条件彼此印证了。

实际使用的时候没有那么麻烦。可以证明，当使用了最优的权重矩阵的时候，GMM 的目标函数渐进服从卡方分布，因而只要检验这个卡方分布就可以了，也就是上面的 J-test。p-value 为0.6884，看来这三个矩条件没有矛盾的地方。

但是一定要注意，即使通过了这个检验，也不代表矩条件一定是成立的，因为有可能三个矩条件都是错的，只不过错的方向是一致的。比如这个例子里面，有可能\(x\)的分布前三阶矩跟正态分布是一样的，但第四阶就不一样了。因而通过这个检验不代表x一定服从正态分布。当然，如果通不过，可以比较自信的说，\(x\)不服从正态分布。

比如，我们把上面的数据生成过程改为 gamma 分布，得到的结果：

p-value 为0.0000，拒绝了原假设，也就是说，三个矩条件不同时成立，数据很有可能不是从正态分布中生成的。

---

计量经济学的很多很多问题基本都可以归结为 GMM 的问题。从最简单的 OLS、2SLS 到稍微复杂一点的面板数据、动态面板等等，本质上都是在找矩条件。比如工具变量的 2SLS，可以发现矩条件不过就是：

\[\mathrm{E}[(y_i-x_i^\prime\beta)z_i]=0\]

套一下上面的公式，最优权重矩阵(的逆)为：

\[\mathrm{E}[(y_i-x_i^\prime\beta_0)z_i z_i^\prime(y_i-x_i^\prime\beta_0)^\prime]=\mathrm{E}[e_i^2z_i z_i^\prime]=\sigma^2\mathrm{E}[z_iz_i^\prime]\]

带入到目标函数中，就得到了 2SLS。

甚至，一些其他的估计量，比如 MLE、M-estimator 等，在一定的条件下也可以转化为 GMM，因为这些估计量的一阶条件可以看成是矩条件。所以 GMM 也就变成了一个统一的框架。

为什么 GMM 这么受欢迎呢？因为 GMM 把复杂的统计过程抽象化成为一个（看似）简单的过程：找矩条件。只要你能找到矩条件，你就能估计。GMM 把估计的繁琐细节全都抽象了，面对一个模型，你所需要做的所有事情就是找到矩条件，证明这个模型是可以识别的，然后什么也不用管，一股脑儿塞进去，结果就出来了。

所以呢如果你去看一些稍微复杂的模型，基本都可以归结为矩条件。

至于题主提到的资产定价，刚好 Gretl 提供了一个可以使用的数据集和 code。资产定价最简单的模型应该就是 C-CAPM 了，其重要结论就可以直接归结为这么一个矩条件：

\[\begin{equation} \mathrm{E}\left[\delta\frac{r_{j,t+1}}{p_{j,t}}\left(\frac{C_{t+1}}{C_t}\right)^{\alpha-1}\Bigg|\mathcal{F}_t\right]=1 \end{equation}\]

其中\(\mathcal{F}_t\)为第\(t\)期所知道的所有信息，包括\(C_t\)、\(r_t\)等等。所以根据这个式子，如果令

\[e_t=\delta\frac{r_{j,t+1}}{p_{j,t}}\left(\frac{C_{t+1}}{C_t}\right)^{\alpha-1}-1\]

那么\(e_t\)跟\(C_t\)、\(r_t\)等等都是正交的，自然可以作为矩条件来用。

Gretl 自带了Hall的数据集，在 user guide 第 206 页开始给出了说明和代码，以及结果，感兴趣的可以去看看，很简单的一个程序。

我猜想上面的两个例子已经足够简单了，特别是正态分布的例子，应该不可能更简单了。

KF CHE：剛開始學 GMM，這個答案幫助很大，萬分感謝。有問題還想請教一下，希望先生有空賜教一下。如果 instrument rank 剛好就和要估計的 estimators 數目一樣，這時是 just-identified，用不著去管 j-stat。於是這時候我就只能用經濟常識去支持我的 instruments 是有效的，而沒有什麼統計工具可以幫忙嗎?

慧航：是的，没有。

Huang Zhibin

GMM 简直是计量的良心，它可以涵盖几乎所有常用的 estimator，OLS, IV, 2SLS, GLS, RE, FE, SUR, 3SLS, Pooled OLS…全是它的特殊情况。所以 LZ 你说用简单的例子解释一下，我瞬间不知道该从何讲起…因为 GMM 的应用…实在广泛了。

LZ 看样子是做宏观或者金融的，那我就来根据 Hayashi 的 econometrics 来大致解释一下 GMM。GMM 是一个 framework，本质是运用矩条件，对参数进行估计。所以我们叫它广义矩估计。

我们先在线性模型

\[y_{i} =x'_{i}\beta +\varepsilon _{i}\]

的框架下讨论，这样比较清晰。假设\(y\)是因变量，\(x\)是原自变量，\(z\)是工具自变量（可以和原自变量一致，也可以不一致），我们定义

\[g_{i}=z_{i}*\varepsilon _{i}\]

所谓矩条件，就是我们假设模型的真实参数和总体，满足这样一个条件：

\[\begin{equation} \mathrm{E}[g(z,\beta)]=0 \end{equation}\]

也就是

\[ \mathrm{E}(z_{i}*(y_{i}-x'_{i}\beta ))=0 \]

然后在这个条件下，我们用某种方法去估计参数\(\beta\)，看上去是不是很混乱？OK 让我们做一个小小的变换，假设向量\(x_i=z_i\)，也就是说工具变量和自变量完全一样。这时候矩条件就变成了：

\[\mathrm{E}(x_{i}*(y_{i}-x'_{i}\beta ))=0\]

回想起来这是啥了没？就是简单的线性投影条件呀！它的 sample analogue 是啥？就是 OLS！好，OLS 首先被装到了 GMM 这个框里。但是当\(z_i\)不完全和\(x_i\)一样的时候呢？那我们就得分类讨论了。

1. 如果\(z_i\)里的变量数量小于\(x_i\)，那就是 under-identified（识别不足），这个时候我们没办法用 GMM 估计。（想想简单 IV 里最基本的估计条件就是 IV 数量比内生变量数量多）
2. 如果\(z_i\)里的变量数量等于\(x_i\)里的，那就是 just-identified（恰好识别），这个时候我们的 sample analogue 和用样本估计参数的方法都很直接而且简单，就是用简单算术平均。定义

\[g_{n}=\frac{1}{n} *\sum_{i=1}^{n}{z_{i}*(y_{i}-x'_{i}\beta) }\]

估计方法就是直接让\(g_{n}=0\)，解出对应的\(\beta\)就好了，没啥花样儿。所以我们很清楚可以看到，恰好识别的时候，GMM Estimator 就是：

\[\hat{\beta } _{\text{GMM}}=(\sum_{i=1}^{n}{z_{i}x'_{i}})^{-1}*(\sum_{i=1}^{n}{z_{i}y_{i}} )\]

是不是很熟悉？YES！就是简单的 IV Estimator，当\(z_i=x_i\)时，就直接变成 OLS Estimator 了。

3. 如果\(z_i\)里的变量数量大于\(x_i\)里的，那就是over-identified（过度识别），这就到了 GMM 不一样的地方了。这时候我们不能直接简单用\(g_{n}=0\)的条件去求解\(\beta\)了，因为这时候我们的矩条件比未知数要多，也就是说方程组里的方程数量比未知数多，一般情况下找不到解。咋办？那我们就找一个解得出来的方程组，并且要让\(g_{n}\)尽量“靠近”零。因为\(g_{n}\)其实是空间里的一个点，所以我们这里用一个小技巧，把这种靠近，定义为最小化\(g_{n}\)这个点，和原点的空间距离。我们定义

\[J(\hat{\beta},\hat{W})=n* g'_{n}(\hat{\beta})\hat{W}g_{n}(\hat{\beta})\]

这个\(J\)就是我们要的距离。\(W\)是一个对称且正定的矩阵，表示我们对这个空间距离的某种度量。当\(W=I\)的时候，我们定义的这个距离就是简单的欧式空间距离。前面乘以一个\(n\)没啥别的意思，是为了某些统计量比较好算…，所以我们估计参数\(\beta\)的方法就是：

\[\hat{\beta}_{\text{GMM}}=\arg\min_{\hat{\beta}}J(\hat{\beta},\hat{W})\]

取一个让距离最小的\(\hat{\beta}\)，就得到了我们要的 GMM 估计量。简单求个导，解一下一阶条件我们就有了显性表达式：

\[\hat{\beta}_{\text{GMM}}=(S'_{zx}\hat{W}S_{zx})^{-1}S'_{zx}\hat{W}S_{zy}\]

其中\(S_{zx}=\sum_{i-=1}^{n}{z_{i}x'_{i}},\;S_{zy}=\sum_{i-=1}^{n}{z_{i}y_{i}}\)，这就是单方程 GMM 的一般解。当我们选取不同的\(W\)矩阵，也就是选择不同的空间距离度量时，GMM 会变成各种我们熟悉的 estimator，比如 2SLS 等等。

以上是关于线性模型的。

更一般的 GMM，其实差别不是很大，无非是去掉了矩条件是线性的这个假设。这时候我们有：

\[\mathrm{E}[g(x,\beta)]=0\]

\(x\)是自变量，\(\beta\)是真实参数，同样我们也是最小化一个空间距离：

\[J(\hat{\beta},\hat{W})=n* g'_{n}(\hat{\beta})\hat{W}g_{n}(\hat{\beta})\]

\[\hat{\beta}_{\text{GMM}}=\arg\min_{\hat{\beta}}J(\hat{\beta},\hat{W})\]

只不过在具体求解的时候，如果\(g\)是一个很复杂的非线性函数的话，那就不一定有解析解，需要用数值逼近，然后渐进方差要用 delta method 计算。（这块 general 的 GMM 具体操作方法我也不是很了解，hayashi 和 hansen 的书上也都没有太多介绍，可以咨询@慧航）

以上是最基本的 GMM 内容，从 0 开始定义。更多的重要内容，包括最优权矩阵，多方程 GMM 等等，还是看书吧。推荐 Bruce Hansen 的 Econometrics，里面关于 GMM 的章节很精练，适合快速阅读快速理解，并且是基于iid sample假设。Hayashi 的 Econometrics 对 GMM 的介绍非常全面，适合进阶阅读，基于ergodic stationary假设，偏时间序列。

参考：

• Hayashi, Econometrics
• Bruce Hansen, Econometrics

J-test 是关于 orthogonal condition，也就是我们的矩条件的 test。在模型的 specification 都成立，我们假设的矩条件都真实成立的情况下，\(J\)值会收敛到一个卡方分布（其实这里就是我之前提到的为什么算\(J\)最优化前面要多乘一个\(n\)的原因！因为可以让\(J\)和卡方分布联系上），这样我们就能用\(J\)做统计检验。所以如果\(J\)太大的话，我们就得怀疑模型是不是错了，是不是有些矩条件错了。这里的直观理解很简单，我们假设了矩条件等于零，那\(n\)很大的时候，样本算出来的和零的距离就不应该太大，不然就不对了。

缄默的老橡树（补充）

今天复习 GMM 的时候想到了一个工具变量的找法很开森，于是愉快地决定强答一发 GMM，然后发现前面三位大神已经把能填的坑都填上了。

找个没填完的小坑，稍微灌点水吧，补充一下@刘澈，没讲完的具体的 GMM 提升精度的方法。

前面大神们提到了，GMM 估计相当于给不同的矩条件赋予了不同的权重，然后才能这个权重得到最小化条件，不同的权重阵其实就对不同的估计量，就像@Huang Zibin说的，“OLS, IV, 2SLS, GLS, RE, FE, SUR, 3SLS, Pooled OLS…全是它的特殊情况”。

那么结果来了，权重矩阵辣么多，要挑不过来，怎么选取最好呢，@慧航也指出了，最优权重阵这样，

\[\left\{\mathrm{E}[g(x_i,\theta)g(x_i,\theta)']\right\}^{-1}\]

当然了，根据 slutsky’s theorem，拿样本模拟总体一般错不了。所以样本模拟最优权重阵的结果就是这样：

\[\left\{\frac{1}{n}\sum\left[g(x_i,\hat{\theta})g(x_i,\hat{\theta})'\right]\right\}^{-1}\]

那么问题来了，要估计最优权重阵就要估计参数，要估计参数就要知道最优权重阵（循环一二起，要估计最优权重阵就要估计参数，要估计参数就要知道最优权重阵…）。不要担心，我们有Hansen（1982）。

1. 第一种叫 one-step GMM，玩不出来我就不玩了呗，没有胡屠夫还不吃带毛猪了，我找不到最优权重阵，我找个过的去权重阵差不多意思意思，反正满足内生性条件之后，大样本性质总归是好的，至于小样本性质，那再说吧。

一般\(W_n=\mathrm{I}_n\)（单位阵）或者\(=\mathrm{inv}(Z’Z)\)（工具变量阵乘积的逆）

2. 第二种叫做 two-step GMM，现在不是根据第一种方法有了参数的一个估计了嘛，那往前再走一步咯，我根据参数得到最优权重阵的一个估计，

\[\left\{\frac{1}{n}\sum\left[g(x_i,\hat{\theta})g(x_i,\hat{\theta})'\right]\right\}^{-1}\]

然后再来一次 GMM 估计嘛。

第一、二种方法有一个小小的缺陷，就是初始权重阵的选取，会影响到参数的数值（numerical value）。

3. 第三种叫做 Iterated Efficient（迭代有效）GMM，怎么讲，2 步迭代不够那 3 步迭代，3 步不够迭代 4 步，总有一步，会得到最优的估计的。那怎么判定是不是差不多最优了呢，一般用这次迭代得到的新参数和上次的参数做差，差充分小的时候，就表示逼近已经很成功了。

4. 第四种方法理解起来复杂，叫做 Continuous-updating （连续更新）GMM。GMM 估计是在最小化方程

\[\min_{\hat{\theta}}\left[\frac{1}{N}\sum_ig(x_i,\hat{\theta})\right]^\prime W\left[\frac{1}{N}\sum_ig(x_i,\hat{\theta})\right]\]

然后最优权重阵

\[W=\left\{\frac{1}{n}\sum\left[g(x_i,\hat{\theta})g(x_i,\hat{\theta})'\right]\right\}^{-1}\]

我们直接代进去嘛，这样这个估计方程里面不就没有\(W\)只有参数了，然后估计参数就好了。

第三第四种方法的解，不依赖初始权重阵。理论上说，第三第四种方法的估计应该是渐进等价的，当然小样本性质可能有所差异。

但要注意，如果矩条件不是线性的，那没啥好说的大家都是非线性参数估计；如果矩条件是个线性的，前三种就是线性估计第四种方法还是非线性估计，相比来说，计算更加繁重，但其有限样本性质要稍好些，另外如果存在弱工具变量的问题，其也相对稳健（robust）。

刘澈（金融）

之前的答案没有针对金融/Asset pricing的，补充一个。

题主看 Cochrane 的 Asset Pricing 学 GMM，是想了解宏观金融。GMM 即是 Hansen and Singleton (1982) 专门为了解决宏观金融模型的参数估计问题开发的；Hansen 因其突出贡献还与其他两位金融经济学家共同获得了 2013 年诺贝尔经济学奖。GMM 被资产定价学者开发以后，由于其泛用性，传播到了经济学的其他各个领域，成为了计量经济学中的一种典型方法。

总的来说，GMM 想解决的是复杂系统中的参数估计问题。对于一个复杂的含参系统，估计其中的参数是很困难的，因为你的估计策略不可能照顾到这个系统的所有特征。GMM 方法提出，如果你的估计策略不能面面俱到，那么退而求其次，你的估计策略至少应当考虑到这个系统最重要的特征。GMM 的精髓就是这种简化的思路。

设想你只有一个简单的含参系统，例如一个线性均值方程\(\mathrm{E}(y|X)=b_0 + b_1X\)。如果你想估计整个系统，那么你只需要估计其中的参数\(b_0\)与\(b_1\)即可。假设方程真实成立，那么想用数据{y, X}估计出\(b_0\)与\(b_1\)非常简单：只需将\(y\)对\(X\)做最简单的线性 OLS 回归即可。

但是设想你的参数系统比较复杂，比如宏观资产定价里最简单的一种 Euler Equation (with power utility)：

\[\begin{equation}\label{eq:zhihuGMM:Liu1} \mathrm{E}_t\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}R_{i,t+1}\right] = 1 \end{equation}\]

其中\(\mathrm{E}_t\)是\(t\)时刻的条件期望，\(R_i\)是市场中任意一种资产的毛收益率，\(C_t\)为\(t\)时刻的消费，\(\beta\)是主观折现因子，\(\gamma\)是风险厌恶系数。如果你想估计整个系统，那么你只需要估计其中的参数\(\beta\)和\(\gamma\)即可。但是很显然，假设你能拿到消费、任意资产的毛收益率等一些经济数据，而且假设经济数据（作为随机变量）真的服从等式，那么一个简单的 OLS 是不能搞定参数估计的。原因很简单，因为这个系统太复杂了。所以，想估计这个系统，就必须简化问题。这个系统复杂的原因在于：

• 式\eqref{eq:zhihuGMM:Liu1}对于市场上的所有资产全都成立。所以实际上式\eqref{eq:zhihuGMM:Liu1}包含了无穷多个方程。但是这个太复杂了，估计出使得式\eqref{eq:zhihuGMM:Liu1}对于所有资产都成立的\(\beta\)和\(\gamma\)很困难。所以我们退而求其次。如果有\(\beta\)和\(\gamma\)会使得式\eqref{eq:zhihuGMM:Liu1}对于所有资产都成立，那么他们也会使得式\eqref{eq:zhihuGMM:Liu1}对你认为的最重要的资产成立。比如，如果你认为一个市场中最重要的资产是市场指数与无风险债券，那么当然式\eqref{eq:zhihuGMM:Liu1}对市场指数与无风险债券均成立，亦即

\[\begin{align} & \mathrm{E}_t\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}R_{m,t+1}\right] = 1\label{eq:zhihuGMM:Liu21}\\ & \mathrm{E}_t\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}\right]R_{f,t} = 1\label{eq:zhihuGMM:Liu22} \end{align}\]

如果估计和就能够成功得到\(\beta\)和\(\gamma\)，那么就估计更为简单的和好了，因为其得到的\(\beta\)和\(\gamma\)也能使\eqref{eq:zhihuGMM:Liu1}成立。

• 但是，估计式\eqref{eq:zhihuGMM:Liu21}和\eqref{eq:zhihuGMM:Liu22}也太复杂了，因为式\eqref{eq:zhihuGMM:Liu21}和\eqref{eq:zhihuGMM:Liu22}仍然用“\(t\)时刻的条件期望”写成：对于任意的时间\(t\)，\eqref{eq:zhihuGMM:Liu21}和\eqref{eq:zhihuGMM:Liu22}式都必须成立。所以式\eqref{eq:zhihuGMM:Liu21}和实际包含了无穷多个方程，这种复杂程度使得我们没法进行参数估计。所以，我们必须进一步简化，简化的方式就是将\eqref{eq:zhihuGMM:Liu21}和\eqref{eq:zhihuGMM:Liu22}中的条件期望\(\mathrm{E}_t[...]\)简化为无条件期望\(\mathrm{E}[...]\)——自然是通过期望迭代定律（Law of Iterated Expectations）实现。但是，如果我直接将条件期望简化为无条件期望，我将无穷多等式简化为两个等式，损失的信息实在太多，这样不好。所以，为了避免在简化的过程中损失过多信息，我们一般会使用一些“工具变量”（instrumental variables）来丰富信息含量。

假设你认为市场中的 Price-dividend ratio 是比较重要的经济变量，你希望在你的估计中体现它，那么你就可以用它来做一个工具变量。记\(t\)时刻的 Price-dividend ratio 为\(z_t\)。式\eqref{eq:zhihuGMM:Liu21}可以变换为：\(z_t\mathrm{E}_t[\beta(\frac{C_{t+1}}{C_t})^{-\gamma}R_{m,t+1} -1] = 0\)，因为\(z_t\)是时刻\(t\)的变量，所以可以进一步变换为\(\mathrm{E}_t[z_t(\beta(\frac{C_{t+1}}{C_t})^{-\gamma}R_{m,t+1} -1)] = 0\)。等式两边使用迭代期望定律，得到无条件期望等式

\[\begin{equation}\label{eq:zhihuGMM:Liu31} \mathrm{E}\left\{z_t\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}R_{m,t+1} -1\right]\right\}= 0 \end{equation}\]

同理，式\eqref{eq:zhihuGMM:Liu22}也可以变换为

\[\begin{equation}\label{eq:zhihuGMM:Liu32} \mathrm{E}\left\{z_t\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}R_{f,t} -1\right]\right\} = 0 \end{equation}\]

这样，我们就进一步将复杂的\eqref{eq:zhihuGMM:Liu21}和\eqref{eq:zhihuGMM:Liu22}简化成了\eqref{eq:zhihuGMM:Liu31}和\eqref{eq:zhihuGMM:Liu32}。

采用一个\(z_t\)，我们将无穷多个式子简化为了两个式子，简化程度很大。为了避免简化程度过大，我们一般会多选用一些工具变量。每选用一个工具变量，就增加两个无条件期望等式。比如，常数变量“1”显然也是一个工具变量。重复上面的操作，我们得到

\[\begin{equation}\label{eq:zhihuGMM:Liu33} \mathrm{E}\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}R_{m,t+1} -1\right]= 0 \end{equation}\]

和

\[\begin{equation}\label{eq:zhihuGMM:Liu34} \mathrm{E}\left[\beta\left(\frac{C_{t+1}}{C_t}\right)^{-\gamma}R_{f,t} -1\right] = 0 \end{equation}\]

所以，为了估计\eqref{eq:zhihuGMM:Liu1}，我们利用合理选用重要资产与工具变量+迭代期望定律的策略将\eqref{eq:zhihuGMM:Liu1}式简化为了几个较为简单的等式，并且选用了多个工具变量（本例为 2 个）来避免简化过度。最终，我们得到式\eqref{eq:zhihuGMM:Liu31}、\eqref{eq:zhihuGMM:Liu32}、\eqref{eq:zhihuGMM:Liu33}、\eqref{eq:zhihuGMM:Liu34}（本例包含 4 个式子/无条件期望等式/“矩条件”）。这个系统中有两个参数，四个等式。等式个数多于待估参数个数，可以进行估计。需要的数据为消费、市场指数收益率、无风险收益率和 Price-dividend ratio。事实上，这就是你建立的 GMM 问题。

为了避免实际计算时可能出现的过度识别（Over-identification）问题，采取@慧航和@Huang Zibin答案中的策略求解\(\beta\)和\(\gamma\)的 GMM 估计量：将\eqref{eq:zhihuGMM:Liu31}、\eqref{eq:zhihuGMM:Liu32}、\eqref{eq:zhihuGMM:Liu33}、\eqref{eq:zhihuGMM:Liu34}简记成\(\mathrm{E}[\mathbf{g}(C, R_f, R_m, z; \beta, \gamma)] = \mathbf{0}\)，这是一个4*1的向量等式。用样本矩\(\bar{\mathbf{g}} = \frac{1}{T}\sum_t g_t\)（平均数）替代总体矩（期望），对于一个4*4维的正定矩阵\(W\)，求解\(\min_{\beta, \gamma} \bar{\mathbf{g}}' W \bar{\mathbf{g}}\)，得到的解即为估计结果。求解一般通过数值方法，另如需提升估计精度可以使用两阶段 GMM、Continuous-updating GMM 等，均数细节，不再赘述。

本例与 Hansen and Singleton(1982) 不尽相同。可补充阅读 Hansen and Singleton(1982)。