回归时交叉项为什么要去平均？ - 慧航 - 专栏

原文地址：https://zhuanlan.zhihu.com/p/26257159

之所以写这篇文章是因为在一个微信群里面的争论。

我想很多人都知道，当我们做回归的时候，如果回归方程里面包含着交叉项，那么一般我们对变量去平均。那么为什么这么做呢？

有的人的解释是消除多重共线性。然而就像我之前写过的一个答案¹一样，在计量经济学领域，如果我们关注的是系数，增大样本几乎是解决多重共线性的唯一方法。其他的方法，要么会导致参数的不一致，要么就是自欺欺人的方法。所以期刊中的文章如果意识到了多重共线性的问题，都不会去讨论，更没有办法去解决这一问题。

至于为什么要去平均，我们不妨稍微写一下线性投影（按照伍德里奇书里面的方法）：

如果不去平均，那么 OLS 是一个线性投影：

\[L(y|x_1,x_2,x_1\cdot x_2)=\beta_1 x_1+\beta_2\cdot x_2 +\gamma x_1\cdot x_2\]

而如果去平均（疑问：中括号中的部分是什么？²）：

\[ \begin{aligned} L(y|\tilde{x}_1,\tilde{x}_2,\tilde{x}_1\cdot \tilde{x}_2) & =b_1 \tilde{x}_1+b_2\cdot \tilde{x}_2 +r\cdot \tilde{x}_1\cdot \tilde{x}_2\\ & =b_1 (x_1-\bar{x}_1)+b_2\cdot (x_2-\bar{x}_2) +r\cdot(x_1-\bar{x}_1)\cdot (x_2-\bar{x}_2)\\ & =b_1x_1-b_1\bar{x}_1+b_2x_2-b_2\bar{x}_2+rx_1x_2-rx_1\bar{x}_2-rx_2\bar{x}_1+r\bar{x}_1\bar{x}_2\\ & =(b_1-r\bar{x}_2)x_1+(b_2-r\bar{x}_1)x_2+rx_1x_2+[r\bar{x}_1\bar{x}_2-b_1\bar{x}_1-b_2\bar{x}_2] \end{aligned} \]

所以其实我们可以得到：

\[ \left\{ \begin{aligned} \beta_1 & =b_1-r\bar{x}_2\\ \beta_2 & =b_2-r\bar{x}_1\\ \gamma & =r \end{aligned}\right. \]

所以实际上，这两种方法计算的系数，可以使用上面三个方程相互计算得到。相应的，系数的标准差也可以使用上面三个方程计算出来。

也就是说，如果做了去平均的回归，那么不去平均的回归结果（包括系数和方差）用上面三个方程就可以算出来了；如果做了不去平均的回归，那么去平均的回归结果（包括系数和方差）用上面三个方程也可以算出来。

所以你跟我说这是解决了多重共线性？逗我呢？

如果再不信，可以做个简单的小模拟：

clear
set obs 100
gen x1=rnormal()*sqrt(2)+1 // mean 1
gen x2=2*x1+rnormal()+1  // mean 3
gen x12=x1*x2
scalar beta1=-3
scalar beta2=-1
scalar gamma=1
gen y=beta1*x1+beta2*x2+gamma*x12+rchi2(2)

// deman
egen mean_x1=mean(x1)
egen mean_x2=mean(x2)
gen demean_x1=x1-mean_x1
gen demean_x2=x2-mean_x2
gen demean_x12=demean_x1*demean_x2

// regression
reg y x1 x2 x12
reg y demean_x1 demean_x2 demean_x12

回归结果：

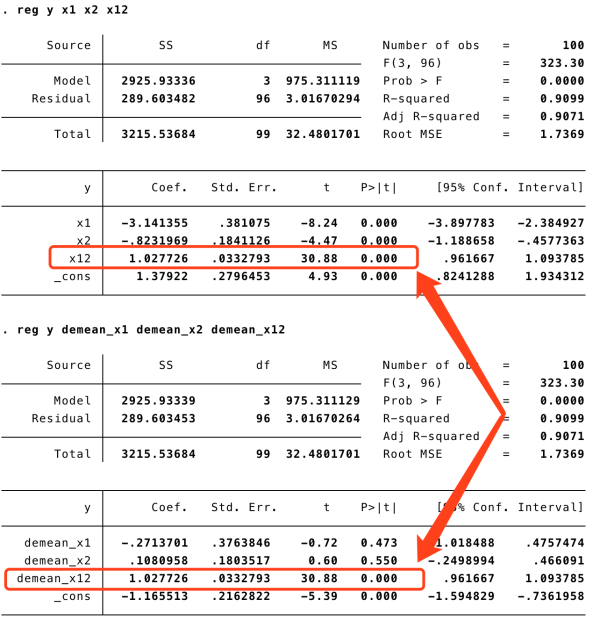
配合着描述性统计：

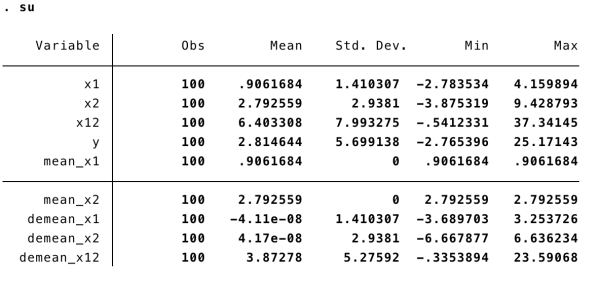
可以轻易的验证上面的三个方程是成立的。

特别是，注意去不去平均，交叉项的系数和标准误都是一样的，所以如果我们只关注交叉项，比如在 DID 里面，去不去平均都可以。

那么这个变换是不是解决了多重共线性问题呢？有的人是这么 argue 的：

你看，相关系数小了很多哎！难道不是解决了多重共线性？

要注意，多重共线性是要看偏相关系数的，实际上，如果我们做这样的回归：

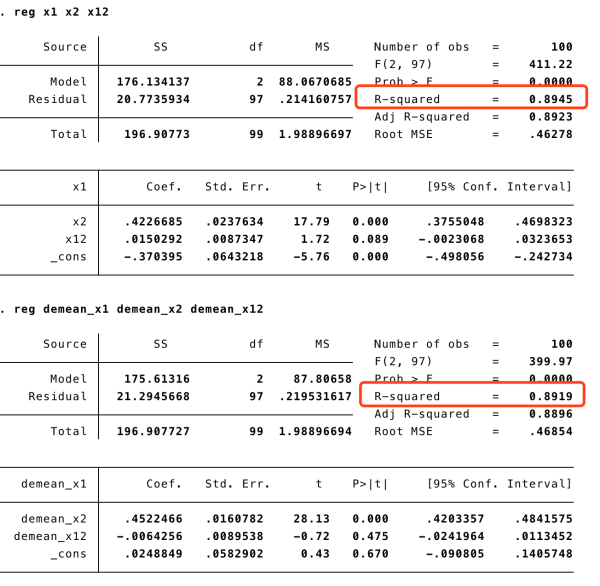
你会发现，两个回归的 R-squared 基本上是一样的。

这不是自欺欺人是干嘛？

也有人说了，去平均之后的确更容易显著啊！难道不是因为多重共线性吗？

不是的。去平均之后更容易显著是因为，去平均之后\(x_1\)和\(x_2\)前面的系数都不一样了，参考我上面写的三个方程的结论，相当于加上了一个系数，所以更容易显著了。当然，这也不是绝对的，比如在上面的模拟里面，我通过一个特殊的设定展示了，去平均之后也有可能更不显著了。

注意我在这里仅仅是说去平均这一做法不是为了解决多重共线性问题，而没有说去平均这个做法是错的。实际上，去平均才是比较标准的做法。

为什么呢？如果我们算一下偏效应：

\[\frac{\partial \mathrm{E}(y|\tilde{x}_1,\tilde{x}_2,\tilde{x}_1\cdot \tilde{x}_2)}{\partial x_1} =b_1 +r\cdot\tilde{x}_2\]

而其期望：

\[\mathrm{E}\left\{\frac{\partial \mathrm{E}(y|\tilde{x}_1,\tilde{x}_2,\tilde{x}_1\cdot \tilde{x}_2)}{\partial x_1}\right\} =b_1\]

也就是说，去平均之后的\(x_1\)的系数才是\(x_1\)对\(y\)的平均影响。

如果我们做出了\(x_1\)的系数不显著，但是交叉项的系数是显著的，说明平均而言\(x_1\)对\(y\)是没有影响的，但是\(x_1\)对\(y\)是有影响的，其影响随着\(x_2\)的不同而变化。只是在总体上平均而言，\(x_1\)对\(y\)没有影响。

所以总结一下，其实去不去平均这两种做法是等价的，只不过去平均之后的系数更容易解释，所以我们一般做回归的时候会去平均处理。这个跟多重共线性没啥关系。

此外多说一句，这个例子也可以回答为什么我们需要做描述性统计。我在这个回答³里面提到过：

除以上原因外，还有个非常重要的原因，就是帮助读者和审稿人阅读回归表格。很多人做回归的时候，出于某些目的会对一些变量 scaling 等等，但是读者和审稿人往往希望知道这些变量的「经济显著性」究竟有多强。仅仅得到一个显著的结果往往是不够的，关心的变量\(x\)变动之后对结果\(y\)究竟有多大影响？因为单位的问题，有些时候往往难以比较。所以经常我们可能关心「当\(x\)变动一个标准差之后，\(y\)有多大的影响」，这个时候就需要使用描述性统计和回归表格结合起来一起看了。还有比如上面的age同时有age^2，那么当年龄增加\(1\)，平均而言会对\(y\)有多大影响呢？这个时候可能会需要age的均值，同样需要诉诸于描述性统计。类似此类的问题，没有描述性统计的情况下，读者是没办法计算的。

这里给我们的一个启发就是，当我们阅读回归表格的时候，特别是遇到交叉项的时候，一定要结合着描述性统计去看。比如，有的回归结果去平均是不显著的，那么会报告不去平均的结果，这个时候如果配合着描述性统计，配合上面的三个式子，就能还原回真正的平均偏效应了。经验丰富的学者在阅读文章的时候是不会被这些小的 tricks 给迷惑的。

最后硬广：欢迎来我的小密圈交流：

李远哲：学统计那一套的时候真没仔细想这个解释性问题，以为标准化变量是机器学习那一套的标准流程，为了做 gradient descent 的时候比较数值稳定才这么做的。

慧航：如果要做 shrinkage 降维之类的时候，那是一定要标准化的，关键是除以标准差而不是去平均。搞计量注重对参数的解释，所以标准化的原因是不一样的。

毛士林：想知道连续变量交乘的经济含义，应该怎么去解释。这种能够解释经济含义吗一般，比如\(x_1\)变动百分之多少，\(x_2\)的调节效应为多少。貌似如果\(x_2\)为 dummy 的话可以，比价容易解释？或者做分组回归，然后对系数差异进行t检验。不知道我之前的做法是否正确，也都是参考已经发表的文章的做法去做的。。

慧航：1) \(x_1\)对\(y\)的影响随着\(x_2\)的大小而不同。2) 系数的经济含义都可以用偏效应这个工具来做，伍德里奇面板数据的前两章一定要好好看。 3) 最好还是放在一个方差里面用 dummy 去检验，不要单独跑回归然后检验。

靠贩剑为生：在还有交叉项的回归中，如果我最关注的是交叉项的系数，例如 \(x_1*x_2\)，那是否在回归的时候一定要加入单独的\(x_1\)项和\(x_2\)项呢？

慧航：一般来说是一定要的！

波波儿爸：你做的偏相关模拟可能有问题。\(x_1\)和\(x_2\)本身强相关，\(demeam\_x_1\) 和 \(demeam\_x_2\) 也强相关，所以两个回归 r-square 都高。期待你能试试用弱相关变量模拟一下？最后两个公式 \(r*demean\_x_2\) 的期望怎么等于 0 的？

慧航：(1) 对，我是为了举反例而已，故意为之；(2) 因为demean, r_hat=r+op(1)。