原文地址:https://cosx.org/2017/05/random-number-generation/
揭秘统计软件如 R,Octave,Matlab 等使用的随机数发生器,然后做一些统计检验,再将其应用到独立随机变量和的模拟中,最后与符号计算得到的精确结果比较。除特别说明外,文中涉及到的随机数都是指伪随机数,发生器都是指随机数发生器。
1 背景
随机数的产生和检验方法是蒙特卡罗方法的重要部分,另外两个是概率分布抽样方法和降低方差提高效率方法。在 20 世纪 40 年代中期,当时为了原子弹的研制,乌拉姆(S.Ulam)、冯诺依曼(J.von Neumann) 和梅特罗波利斯(N. Metropolis) 在美国核武器研究实验室创立蒙特卡罗方法。当时出于保密的需要,与随机模拟相关的技术就代号“蒙特卡罗”。早期取得的成果有产生随机数的平方取中方法,取舍算法和逆变换法等。这两个算法的内容见统计之都王夜笙的文章。
2 随机数生成
讲随机数发生器,不得不提及一个名为 Mersenne Twister(简称 MT)的发生器,它的周期长达$2^{19937}-1$, 现在是 R 、Octave 和 Matlab 等软件(较新版本)的默认随机数发生器1。
Matlab 通过内置的 rng 函数指定不同的发生器,其中包括 1995 年 Matlab 采用 George Marsaglia 在 1991 年提出的借位减(subtract with borrow,简称 SWB)发生器。在 Matlab 中,设置如下命令可指定发生器及其状态,其中 1234 是随机数种子,指定发生器的状态,目的是重复实验结果,v5uniform 是发生器的名字。
rng(1234, 'v5uniform')Octave 通过内置的 rand 函数指定发生器的不同状态,为获取相同的两组随机数,state 参数的设置一样,如 1234(你也可以设置为别的值)。Octave 已经放弃了老版本内置的发生器,找不到命令去指定早期的发生器,这个和 Matlab 不一样。
rand ('state',1234)
rand(1,5)
0.9664535 0.4407326 0.0074915 0.9109760 0.9392690
rand ('state',1234)
rand(1,5)
0.9664535 0.4407326 0.0074915 0.9109760 0.9392690Python 的 numpy 模块也采用 MT 发生器,类似地,通过如下方式获得相同的两组随机数
import numpy as np
a = np.random.RandomState(1234)
a.rand(5)
array([ 0.19151945, 0.62210877, 0.43772774, 0.78535858, 0.77997581])
a = np.random.RandomState(1234)
a.rand(5)
array([ 0.19151945, 0.62210877, 0.43772774, 0.78535858, 0.77997581])R 的默认发生器也是 MT 发生器,除了设置随机数种子的 seed 参数,还可以通过 kind 参数指定其他发生器,normal.kind 参数指定产生正态分布随机数的发生器,下面也使用类似的方式产生两组完全一样的随机数。
set.seed(seed, kind = NULL, normal.kind = NULL)
set.seed(1234,kind = "Mersenne-Twister", normal.kind = "Inversion") # 默认参数设置
runif(5)
[1] 0.1137034 0.6222994 0.6092747 0.6233794 0.8609154
set.seed(1234,kind = "Mersenne-Twister", normal.kind = "Inversion") # 默认参数设置
runif(5)
[1] 0.1137034 0.6222994 0.6092747 0.6233794 0.8609154SWB 发生器中“借位相减”步骤是指序列的第 \(i\) 个随机数$z_{i}$要依据如下递推关系产生,$$z_{i}=z_{i+20}-z_{i+5}-b$$ 下标$i,i+20,i+5$都是对 32 取模的结果,$z_{i+20}$与$z_{i+5}$做减法运算,\(b\) 是借位,其取值与前一步有关,当$z_i$是正值时,下一步将 \(b\) 置为 0,如果计算的$z_i$是负值,在保存$z_i$之前,将其值加 1,并在下一步,将 \(b\) 的值设为$2^{-53}$。
下面关于随机数生成的效率和后面的统计检验,都以生成$2^{24}$个为基准,是 1600 多万个,取这么多,一方面为了比较编程语言实现的发生器产生随机数的效率,另一方面是后面的游程检验需要比较大的样本量。
Matlab 内置的发生器及大部分的函数,底层实现都是 C 或者 Fortran,MathWorks 创始人 Cleve B. Moler 是数值分析领域著名的 LINPACK 和 EISPACK 包的作者之一,他当年做了很多优化和封装,进而推出 Matlab,只要是调用内置函数,效率不会比 C 差,自己写的含有循环、判断等语句的代码,性能就因人而异了,对大多数人来说,性能要比 C 低。这里比较 Matlab 内置SWB发生器(就当作是 C 语言实现的好了)和用 Matlab 重写的 SWB 发生器的效率,代码如下:
% matlab code
tic % 大约几秒
rng(1234, 'v5uniform') % 调用SWB发生器
x = rand(1,2^24);
toc% octave code
id = tic % 时间耗费大约一小时
randtx('state',0)
x = randtx(1,2^24);
toc (id)randtx不是 Matlab 和 Octave 内置的函数,而是 Cleve B. Moler 基于 Matlab 实现的 SWB 发生器,也是 100 多行包含嵌套循环等语句的 Matlab 代码打包的函数,上面的代码运行时间差异之大也就不难理解了,为了能在 Octave 上跑,我做了少量修改,Octave 软件版本为 4.2.1,安装 Octave 时,Blas 选择 OpenBlas,为了后续检验,在获得随机数后,将其保存到磁盘文件 random_number.mat
save -mat random_number.mat x R,Octave,Matlab 和 Python 内置的发生器都是 MT 发生器,与之实现有关的数学库,也是 Blas,虽然有开源和进一步优化的商业版本之分,但是矩阵乘法,向量乘法之类运算的效率也就半斤八两,Julia 语言官网给出了一个标准测试2。
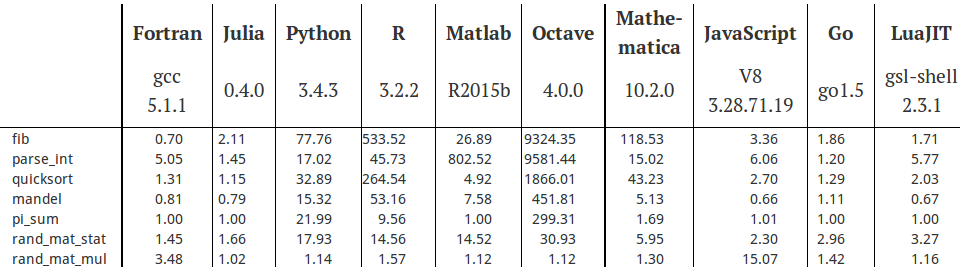
不同语言的性能表现(C 语言在算法中的表现为基准,时间记为 1.0)
这里再给出用C语言实现的 MT 发生器,产生同样多的随机数,只需要 10 秒左右,其中包含编译和写随机数到文件的时间,实际产生随机数的时间应该远小于这个时间。(程序运行环境环境 Dev-C++ 5.11,用 64 位的 GCC 编译)。
3 统计检验
随机数的检验是有一套标准的,如 George Marsaglia 开发的 DieHard 检验程序,检验的内容很丰富。这篇文章只能算初窥门径,R 内产生真随机数的包是 Dirk Eddelbuettel 开发的 random包,它是连接产生真随机数网站的接口。
3.1 相关性检验
先来一个简单的,就用 R 产生的两个独立同均匀分布样本,调用 cor.test 做相关性检验,看看这两组数是不是足够独立同分布,通过眼球验证,随着样本量增大,相关性趋于 0,相关性弱到可以视为独立。如下图所示
library(ggplot2)
library(viridisLite)
library(viridis)
set.seed(1234)
corr <- rep(0, 1000)
for(i in seq(from = 1000, to = 1000000, by = 1000)) {
corr[i/1000] <- cor.test(runif(i, min = 0, max = 1),
runif(i, min = 0, max = 1))$estimate}
ggplot(data.frame(x = seq(1000), y = corr), aes(x = x, y = y)) +
geom_hex(show.legend = FALSE) +
scale_fill_viridis(direction = -1) + xlab("Sample size *10^3") + ylab("Correlation") 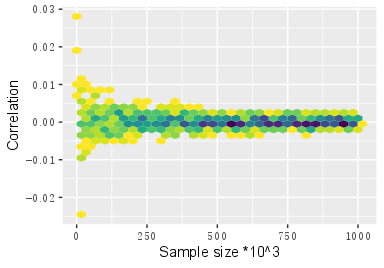
image
3.2 分布检验
检验产生的随机数是否服从指定的分布:原假设是样本来自指定的分布,计算的 P 值比较大,就不能拒绝原假设。
ks.test(runif(1000), "punif") # 分布检验
##
## One-sample Kolmogorov-Smirnov test
##
## data: runif(1000)
## D = 0.022302, p-value = 0.7025
## alternative hypothesis: two-sided检验两样本是否来自同一分布:原假设是两样本来自同一分布,计算的P值比较小,就表示两样本不是来自同一分布。
ks.test(runif(1000), runif(1000)) # 同分布检验
##
## Two-sample Kolmogorov-Smirnov test
##
## data: runif(1000) and runif(1000)
## D = 0.04, p-value = 0.4005
## alternative hypothesis: two-sided从结果来看,R内置的随机数发生器通过了检验(嘿嘿,这是肯定的!!)。
3.3 游程检验
游程检验对随机数序列的随机性检验,不对序列做任何分布假设,不同于上面的相关性检验和省略没讲的特征统计量(如均值和方差)的检验。先对随机性略作解释,简单起见,我们考虑 0-1 序列,抛掷均匀的硬币 1000 次,正面向上记为 1,反面向上记为 0,这是一个离散的均匀分布,每一次抛掷硬币都无法准确地判断出现的是正面还是反面,若记录的序列中 0 和 1 相对集中的出现,不是随机,0 和 1 交替出现,呈现周期性也不是随机,除了这两种情况基本就是随机了。
游程检验的原假设是序列满足随机性,序列一旦生成,就是有序的,因为游程检验需要固定位置,再数上升(下降)的游程数,当计算的 P 值比较大时,不能拒绝原假设,即不能否认这个序列是随机的。对上述 0-1 序列进行模拟,然后检验,如下所示
library(tseries)
x <- sample(c(0, 1), 1000, replace = TRUE, prob = c(1/2, 1/2))
runs.test(factor(x))
##
## Runs Test
##
## data: factor(x)
## Standard Normal = 0.45116, p-value = 0.6519
## alternative hypothesis: two.sided现在用游程检验比较 SWB 发生器(Octave/Matlab 版)、MT 发生器(R 语言版)和 MT 发生器(C 语言版)。对于一般的实数序列,得先指定一个阈值,记为 delta,然后比较序列中的值和 delta 的大小关系,这里类似数上升或下降的游程长度(runs length),基于这样一个事实:如果序列表现随机,则序列中两个小于 delta 的值,间隔越远出现的次数越少。可以这样理解,还是以上面抛硬币的例子来说,出现了很多次正面,那么下一次抛掷倾向于出现反面,这是一条人人可接受的经验。
为了把这条经验可视化出来,对序列做如下操作:先给定阈值 delta 为 0.01(也可以取别的值),取出序列中的值小于 delta 的位置,位置序列前面添加 0,再差分,然后每个值减 1,得到新序列,新序列中的值为 0,表明原序列连续两个值小于 delta,新序列中的值为1,表明间隔 1 个数小于 delta,新序列中的值为 2,表明间隔 2 个数小于 delta,依次类推…..统计所有的情况,用直方图显示,这就获得游程长度与间隔的关系图(间隔数取到 100 足可示意)。
library(gridExtra)
library(R.matlab)
# 游程频数直方图
run_test_fun <- function(x, string, delta) {
n <- length(x)
len <- diff(c(0, which(x < delta), n + 1)) - 1
ggplot(data.frame(x = len[len < 101]), aes(x, fill = ..count..)) +
scale_fill_viridis(direction = -1) +
geom_histogram(binwidth = 1, show.legend = FALSE) +
xlab(string) + ylab("")
}
set.seed(1234) # R默认采用Mersenne Twister发生器
r_data <- runif(2^24, 0, 1); # R内生成均匀分布随机数
matlabv5_data <- readMat("random_number.mat") # 读取Octave生成的均匀分布随机数
temp <- read.table(file = "random_number.txt") # 读取C语言生成的均匀分布随机数
c_data <- c(as.matrix(t(temp)))
p1 <- run_test_fun(x = r_data, string = "R", delta = 0.01)
p2 <- run_test_fun(x = matlabv5_data$x, string = "Matlab v5", delta = 0.01)
p3 <- run_test_fun(x = c_data, string = "C", delta = 0.01)
grid.arrange(p1, p2, p3, ncol=3)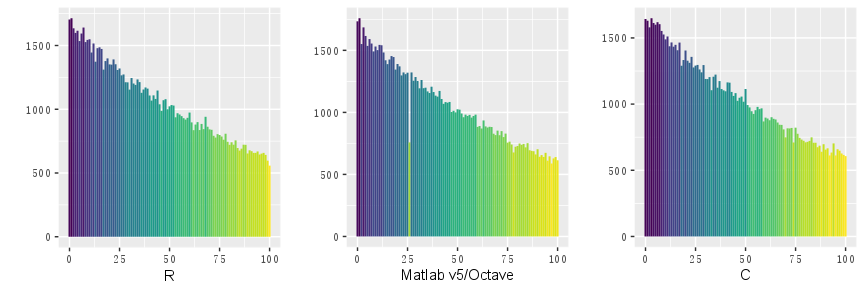
image
从图中可以看出 MT 发生器通过了检验,SWT 发生器没有通过,在间隔数为 27 的位置,有一条沟,按规律游程长度不应该减少这么多,这是因为 SWB 发生器“借位减”步骤,取模 32 的运算和 5 一起消耗了间隔为 27 的数量(读者可以按借位减的递推关系思考是如何消耗的),导致不符合随机性的要求,该算法细节参见 Cleve B. Moler的书《Numerical Computing with MATLAB》第 9 章第 267 页 。
4 应用
4.1 两个均匀分布的统计模拟
随机变量 $X_{1},X_{2}\stackrel{iid}{\sim}$某分布(比如二项分布,泊松分布,正态分布,指数分布,卡方分布,伽马分布),则$X_{1}+X_{2}$也服从该分布。常见的均匀分布是否具有这样的可加性?具体地说,就是$X_{1},X_{2}\stackrel{iid}{\sim}U(0,1)$ ,$X_{1}+X_{2}$ 是否服从$U(0,2)$ ? 如果有一台电脑在旁边,我首先想到的就是敲三五行代码,画个散点图、直方图,看图说话。
set.seed(1234)
x <- runif(10000, min = 0, max = 1)
y <- runif(10000, min = 0, max = 1)
z <- x + y
plot(z) # 散点图
hist(z) # 直方图为美观起见,从 viridis 包调用 viridis 调色板,颜色越深的地方,相应的数值越大,不管是此处 geom_hex 绘制的六角形热图,还是 geom_histogram 绘制的直方图,都遵循这个规律。
ggplot(data.frame(x = seq(10000), y = z), aes(x = x, y = y)) +
geom_hex(show.legend = FALSE) +
scale_fill_viridis(direction = -1) + xlab("") + ylab("")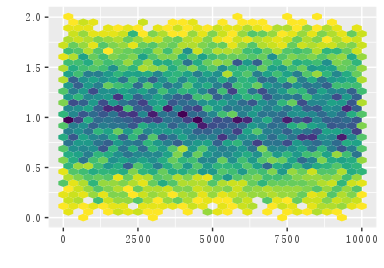
image
显然这不是均匀分布,在 $z=1$ 处,散点比较集中,看起来有点像正态分布。如果往中心极限定理上靠,将作如下标准化$$Y_{2}^{\star}=\frac{X_1 + X_2 - 2*\frac{1}{2}}{\sqrt{\frac{1}{12}}*\sqrt{2}}=\sqrt{6}(X_1 + X_2 -1)$$ 则$Y_{2}^{\star}$的期望为 0,方差为 1。
p4 <- ggplot(data.frame(x = z), aes(x, fill = ..count..)) +
scale_fill_viridis(direction = -1) +
geom_histogram(bins=20, show.legend = FALSE) + xlab("") + ylab("")
p5 <- ggplot(data.frame(x = sqrt(6)*(z-1)), aes(x, fill = ..count..)) +
scale_fill_viridis(direction = -1) +
geom_histogram(bins = 20, show.legend = FALSE) + xlab("") + ylab("")
grid.arrange(p4, p5, ncol=2)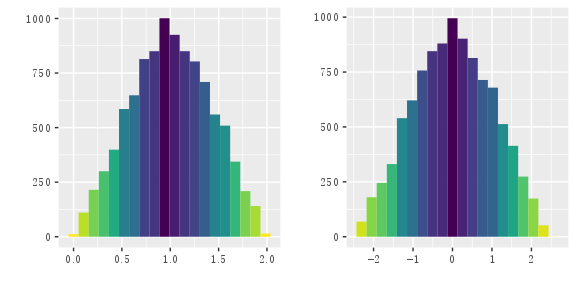
image
只是变换后的图像和之前基本一致,那么现在看来眼球检验不好使了,那就上$P$值呗!
ks.test(sqrt(6)*(z-1), "pnorm") # 分布检验
##
## One-sample Kolmogorov-Smirnov test
##
## data: sqrt(6) * (z - 1)
## D = 0.025778, p-value = 3.381e-06
## alternative hypothesis: two-sided也不是正态分布,既然如此,那就在两个随机变量的情况下,把精确分布推导出来。
4.2 精确分布的推导及计算
课本如《概率论与数理统计教程》 采用卷积的方法求分布函数,这种方法实行起来比较繁琐,也不利于后续编程,下面考虑用特征函数的方法求。我们知道标准均匀分布的特征函数$$\varphi(t)=\frac{e^{it}-1}{it}$$考虑$X_1$和$X_2$相互独立,它们的和用$S_2$表示,则随机变量$S_2$的特征函数为 $$\varphi_2(t)=\varphi(t)*\varphi(t)=(\frac{e^{it}-1}{it})^2=\frac{2(1-\cos(t))e^{it}}{t^2}$$
只要满足条件
$$\int_{-\infty}^{+\infty}\vert \varphi_2(t) \vert \mathrm{d} t < \infty$$
$S_2$的密度函数就可以表示为
$$p_2(x)=\frac{1}{2 \pi}\int_{-\infty}^{+\infty}\mathrm{e}^{-itx}\varphi_2(t)\mathrm{d}t$$
经计算 $$\int_{-\infty}^{+\infty}\vert \varphi_2(t) \vert \mathrm{d} t=4\int_{0}^{+\infty}\frac{1-\cos(t)}{t^2}\mathrm{d}t=4\int_{0}^{+\infty}\big(\frac{\sin(x)}{x}\big)^2\mathrm{d}x=2\pi$$
那么 $$p_2(x)=\frac{1}{2 \pi}\int_{-\infty}^{+\infty}\mathrm{e}^{-itx}\varphi_2(t)\mathrm{d}t=\frac{2}{\pi}\int_{0}^{+\infty}\frac{(1-\cos(t))\cos(t(1-x))}{t^2}\mathrm{d}t=\frac{2}{\pi}\int_{0}^{+\infty}\cos\big(2(1-x)t\big)\big(\frac{\sin(t)}{t}\big)^2\mathrm{d}t$$
一般地,\(n\) 个独立随机变量的和
$$\varphi_n(t)=\big(\frac{e^{it}-1}{it}\big)^n=\big(\frac{\sin(t/2)\mathrm{e}^{\frac{it}{2}}}{t/2}\big)^n$$ 那么,同理 $$p_n(x)=\frac{2}{\pi}\int_{0}^{+\infty}\cos\big(2(n/2-x)t\big)(\frac{\sin(t)}{t})^n\mathrm{d}t$$
要说数值计算一个$p(x)$近似值,是一点问题没有!且看
integrate(function(t,x,n) 2/pi*cos((n-2*x)*t)*(sin(t)/t)^n ,x = 1,n = 2,
lower = 0,upper = Inf,subdivisions = 1000)
## 0.9999846 with absolute error < 6.6e-05 那如果要把上面的积分积出来,获得一个精确的表达式,在$n=2$的时候还可以手动计算,主要使用分部积分,余弦积化和差公式和一个狄利克雷积分公式$\int_{0}^{+\infty}\frac{\sin(ax)}{x}\mathrm{d}x=\frac{\pi}{2}\mathrm{sgn}(a)$,过程略,最后算得
$$p_2(x)=\frac{1}{2}\big((2-x)\mathrm{sgn}(2-x)-x\mathrm{sgn}(-x)\big)-(1-x)\mathrm{sgn}(1-x)=\frac{1}{2}(\left | x \right |+\left | x-2 \right |)-\left | x-1 \right |,0<x<2$$
$p_2(x)$的密度函数图象如下:
fun_p2_1 <- function(x) { 1 / 2 * (abs(x - 2) - 2 * abs(x - 1) + abs(x)) }
fun_p2_2 <- function(x) {
x <- as.matrix(x)
tempfun <- function(x) {
integrate(function(t, x, n) 2 / pi * cos((n - 2 * x) * t) * (sin(t) / t) ^ n,
x = x, n = 2,lower = 0, upper = Inf, subdivisions = 1000)$value
}
return( sapply(x,tempfun) )
}
ggplot(data.frame(x = c(0, 2)), aes(x = x)) +
stat_function(fun = fun_p2_2, geom = "point", colour = "#2A768EFF") +
stat_function(fun = fun_p2_1, geom = "line", colour = "#78D152FF") 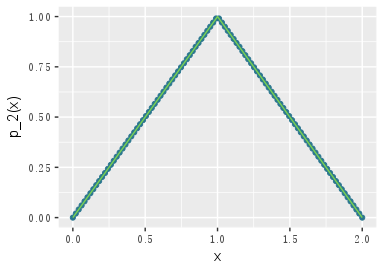
image
从图中可以看出,两种形式的密度函数在数值计算的结果上很一致,当 $n=100,1000$ 时,含参量积分的表示形式就很方便啦!任意给定一个 \(n\),符号计算上面的含参量积分,这个时候还是用软件计算比较合适,R 的符号计算仅限于求导,积分运算需要借助 Ryacas,rSymPy,可惜的是,这些包更新缓慢,即使 $\int_{0}^{+\infty}\frac{\sin(at)}{t}\mathrm{d}t$ 也算不出来,果断直接使用 Python 的 sympy 模块
from sympy import *
a=symbols('a', real = True)
t=symbols('t', real = True, positive = True)
print(integrate(sin(a*t)/t, (t, 0, oo)))
## Piecewise((pi/2, Eq(Abs(periodic_argument(polar_lift(a)**2, oo)), 0)), (Integral(sin(a*t)/t, (t, 0, oo)), True))。。。初次见到这样的结果,是不是一脸mb,翻译一下,就是
$$ \begin{equation*} \begin{cases} \frac{\pi}{2} & \text{for}\: \left|{\operatorname{periodic_{argument}}{\left (\operatorname{polar\_lift}^{2}{\left (a \right )},\infty \right )}}\right| = 0 \\ \int\limits_{0}^{\infty} \frac{1}{t} \sin{\left (a t \right )}\, dt & \text{otherwise} \end{cases} \end{equation*} $$
稍为好点,但是还是有一大块看不懂,那个绝对值里是什么3?还是不要纠结了,路远坑多,慢走不送啊!话说要是计算$p_2(x)$密度函数里的积分,
from sympy import *
x=symbols('x', real=True)
t=symbols('t', real=True,positive=True)
print(integrate(2/pi*cos(2*t*(1-x))*(sin(t)/t)**2,(t,0,oo)))
## Piecewise((Piecewise((2*x, (2*x - 2)**2/4 < 1), (0, 4/(2*x - 2)**2 < 1), (meijerg(((1/2,), (1, 1, 3/2)), ((1/2, 1, 0), (1/2,)), polar_lift(-2*x + 2)**2/4), True))/2, Eq(Abs(periodic_argument(polar_lift(-2*x + 2)**2, oo)), 0)), (Integral(2*sin(t)**2*cos(2*t*(-x + 1))/(pi*t**2), (t, 0, oo)), True))那就更长了。。。
$$ \begin{equation*} \begin{cases} \frac{1}{2} \begin{cases} 2 x & \text{for}\: \frac{1}{4} \left(2 x - 2\right)^{2} < 1 \\ 0 & \text{for}\: \frac{4}{\left(2 x - 2\right)^{2}} < 1 \\ {G_{4, 4}^{3, 1}\left(\begin{matrix} \frac{1}{2} & 1, 1, \frac{3}{2} \\\frac{1}{2}, 1, 0 & \frac{1}{2} \end{matrix} \middle| {\frac{1}{4} \operatorname{polar\_lift}^{2}{\left (- 2 x + 2 \right )}} \right)} & \text{otherwise} \end{cases} & \text{for}\: \left|{\operatorname{periodic_{argument}}{\left (\operatorname{polar\_lift}^{2}{\left (- 2 x + 2 \right )},\infty \right )}}\right| = 0 \\ \int\limits_{0}^{\infty} \frac{2}{\pi t^{2}} \sin^{2}{\left (t \right )} \cos{\left (2 t \left(- x + 1\right) \right )}\, dt & \text{otherwise} \end{cases} \end{equation*} $$
sympy 模块还是比较强的,化简可能比较弱,感觉是我的条件声明没有充分利用,要看懂,得知道一些复变函数的知识,这个时候,可以试试 Maple 或者 Mathematica,面对高昂的费用,我们可以使用在线的免费计算 WolframAlpha(http://www.wolframalpha.com/),输入
integrate 2/pi*cos(2*t*(1-x))*(sin(t)/t)^2 ,t ,0,oo即可得$p_2(x)=\frac{1}{2}(\left | x-2 \right |-2\left | x-1 \right |+\left | x \right |)$,\(n\) 取任意值都是可以算的,由于式子比较复杂,就不展示了。
5 小结
作者的一些经验感悟:
因为看论文的原因(感觉 MCMC 好像哪都有),接着从随机数生成开始自学 MCMC,一次偶然的机会,去年在北京计算科学研究中心听清华喻文健教授的报告,提到均匀分布的随机数检验,中间也出现了这个图,现在已经记不得是喻教授因为时间原因,没细讲背后的原因,还是自己没听懂,总之只觉得挺有意思的(涉及统计中的游程检验,周围基本都是工科学生,我想我听的更明白些),就记下来,在听报告之前,囫囵地看了康崇禄写的《蒙特卡罗方法理论和应用》的前两章(前两章故事比较多因此看完了),这本书没讲那个例子,却把背后的原因讲明白了(后来细看才知道的)。错位相减算法曾出现在 Matlab,自然就去读 Cleve B. Moler 写的《Numerical Computing with MATLAB》(Revised in 2013),这本书在文中有出现,也介绍了 Matlab 这么多年内置的随机数发生器的变化史。其实还是推荐看康崇禄那本,不仅因为故事多,而且内容全面和透彻,可以挑自己需要和感兴趣的部分读,也不拘泥于 Matlab。
关于应用部分的举例,源于面试,陷于教材,钟于符号计算。这部分涉及一本广为人知的教材《概率论与数理统计教程》(第二版)茆诗松、程依明和濮晓龙著,这本书给了用卷积求独立随机变量和的例子,后面讲特征函数,说它在求独立随机变量和有优势,但是没有举例,所以正好是补充,而且意外地简洁和统一。符号计算获得精确结果是为了和数值计算的结果比较,之前在统计之都的投名状就是符号计算与 R 语言,但是没有提及 Python 的
sympy,这下也正好合体了。
现在,R、Octave 和 Matlab 这些软件没有单纯用借位相减算法来产生随机数,1995 年后,Matlab 使用延迟斐波那契和移位寄存器的组合发生器,直到 2007 年,Matlab 推出 7.4 版本的时候才采用 MT 发生器。↩
在官网的 High-Performance JIT Compiler 部分↩
Python 的符号计算模块
sympy功能比较全,但是化简比较弱,导致结果理解起来不是很方便,比如式子的第一行,看似当$0<x<2$时,$p_{2}(x)=x$是错的,正确的范围应该是$0<x<1$,其实for后面的函数polar_lift()要求参数大于 \(0\),这样就没问题了,建议多撸一撸sympy官方文档。↩