原文地址：http://xymlife.com/2016/05/22/python_mro/

Python: 多继承模式下 MRO(Method Resolution Order) 的计算方式感觉表达式有问题，看不太明白，通过本文也可以大致理解 C3，所以不再看“计算方式”一文。

前言

MRO（Method Resolution Order）：方法解析顺序。

Python 语言包含了很多优秀的特性，其中多重继承就是其中之一，但是多重继承会引发很多问题，比如二义性，Python 中一切皆引用，这使得他不会像 C++ 一样使用虚基类处理基类对象重复的问题，但是如果父类存在同名函数的时候还是会产生二义性，Python 中处理这种问题的方法就是 MRO。

历史中的 MRO

如果不想了解历史，只想知道现在的 MRO 可以直接看最后的 C3 算法，不过 C3 所解决的问题都是历史遗留问题，了解问题，才能解决问题，建议先看历史中 MRO 的演化。

Python2.2以前的版本：经典类（classic class）时代

经典类是一种没有继承的类，实例类型都是type类型，如果经典类被作为父类，子类调用父类的构造函数时会出错。这时 MRO 的方法为DFS（深度优先搜索（子节点顺序：从左到右））。

Class A:   # 是没有继承任何父类的
    def __init__(self):
        print "这是经典类"

inspect.getmro(A)可以查看经典类的 MRO 顺序

import inspect
class D:
    pass

class C(D):
    pass

class B(D):
    pass

class A(B, C):
    pass

if __name__ == '__main__':
    print inspect.getmro(A)
    
>>  (<class __main__.A at 0x10e0e5530>, <class __main__.B at 0x10e0e54c8>, <class __main__.D at 0x10e0e53f8>, <class __main__.C at 0x10e0e5460>)

MRO 的 DFS 顺序如下图：

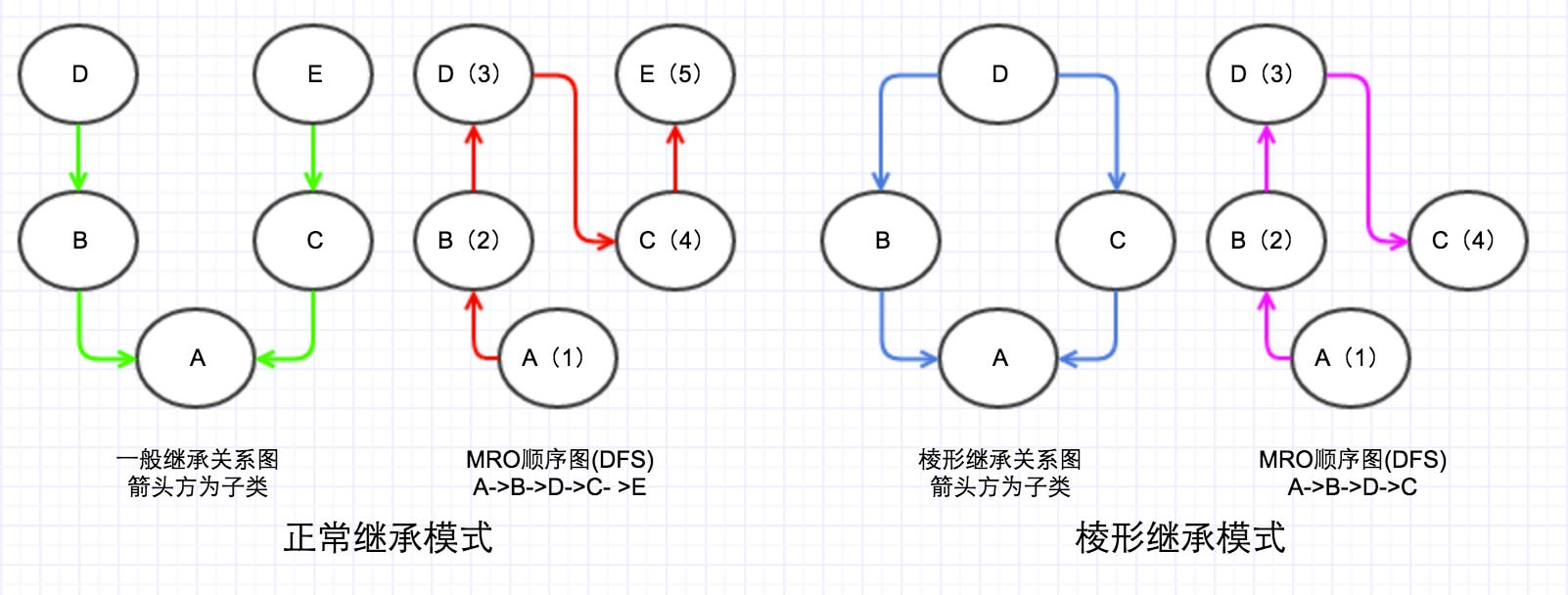
DFS

两种继承模式在DFS下的优缺点

正常继承模式，两个互不相关的类的多继承，这种情况 DFS 顺序正常，不会引起任何问题；
棱形继承模式，存在公共父类（D）的多继承（有种D字一族的感觉），这种情况下 DFS 必定经过公共父类（D），这时候想想，如果这个公共父类（D）有一些初始化属性或者方法，但是子类（C）又重写了这些属性或者方法，那么按照 DFS 顺序必定是会先找到D的属性或方法，那么C的属性或者方法将永远访问不到，导致C只能继承无法重写（override）。这也就是为什么新式类不使用 DFS 的原因，因为他们都有一个公共的祖先object。

Python2.2版本：新式类（new-style class）诞生

为了使类和内置类型更加统一，引入了新式类。新式类的每个类都继承于一个基类，可以是自定义类或者其它类，默认承于object。子类可以调用父类的构造函数。

这时有两种 MRO 的方法1. 如果是经典类 MRO 为 DFS（深度优先搜索（子节点顺序：从左到右））。2. 如果是新式类 MRO 为 BFS（广度优先搜索（子节点顺序：从左到右））。

Class A(object):   # 继承于object
    def __init__(self):
        print "这是新式类"

A.__mro__ # 可以查看新式类的顺序

MRO 的 BFS 顺序如下图：

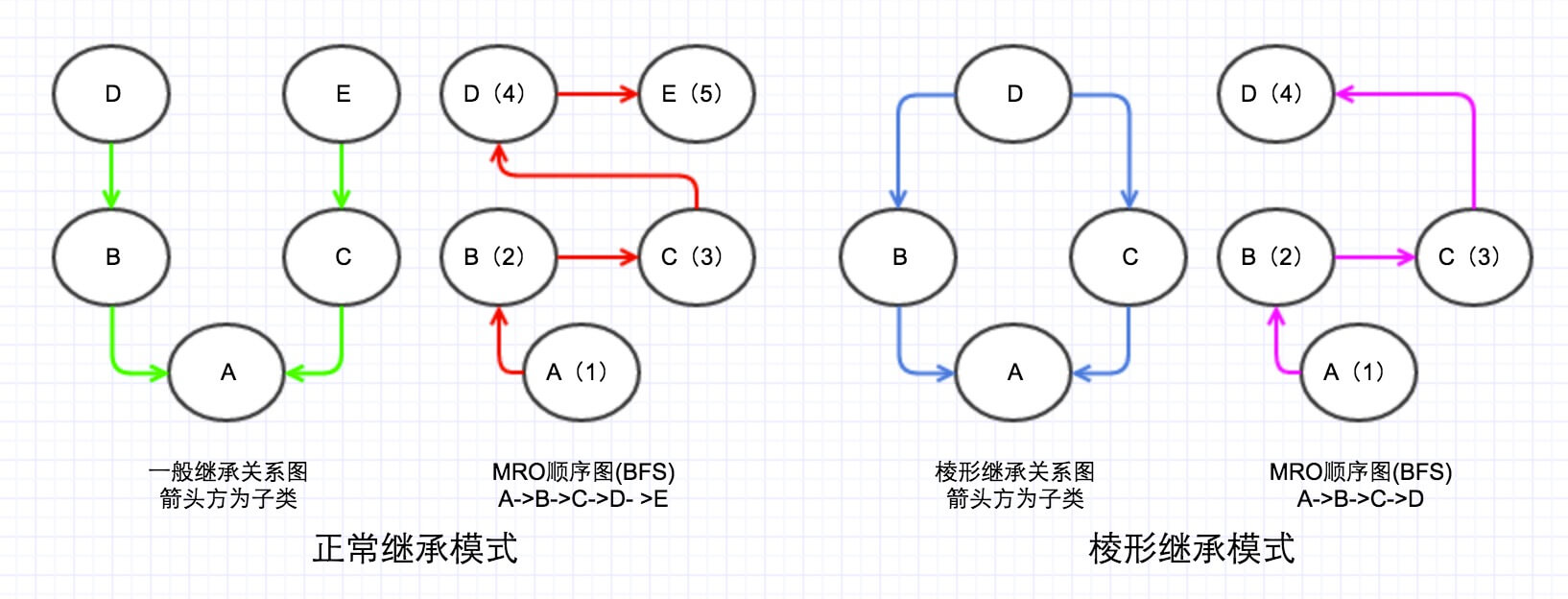
BFS

两种继承模式在 BFS 下的优缺点

正常继承模式，看起来正常，不过实际上感觉很别扭，比如B明明继承了D的某个属性（假设为foo），C中也实现了这个属性foo，那么 BFS 明明先访问B然后再去访问C，但是为什么foo这个属性会是C？这种应该先从B和B的父类开始找的顺序，我们称之为单调性。
棱形继承模式，这种模式下面，BFS 的查找顺序虽然解了 DFS 顺序下面的棱形问题，但是它也是违背了查找的单调性。因为违背了单调性，所以 BFS 方法只在Python2.2中出现了，在其后版本中用C3算法取代了 BFS。

Python2.3 到 Python2.7：经典类、新式类和平发展

因为之前的 BFS 存在较大的问题，所以从 Python2.3 开始新式类的 MRO 取而代之的是 C3 算法，我们可以知道 C3 算法肯定解决了单调性问题，和只能继承无法重写的问题。C3 算法具体实现稍后讲解。

MRO 的 C3 算法顺序如下图：看起简直是 DFS 和 BFS 的合体有木有。但是仅仅是看起来像而已。

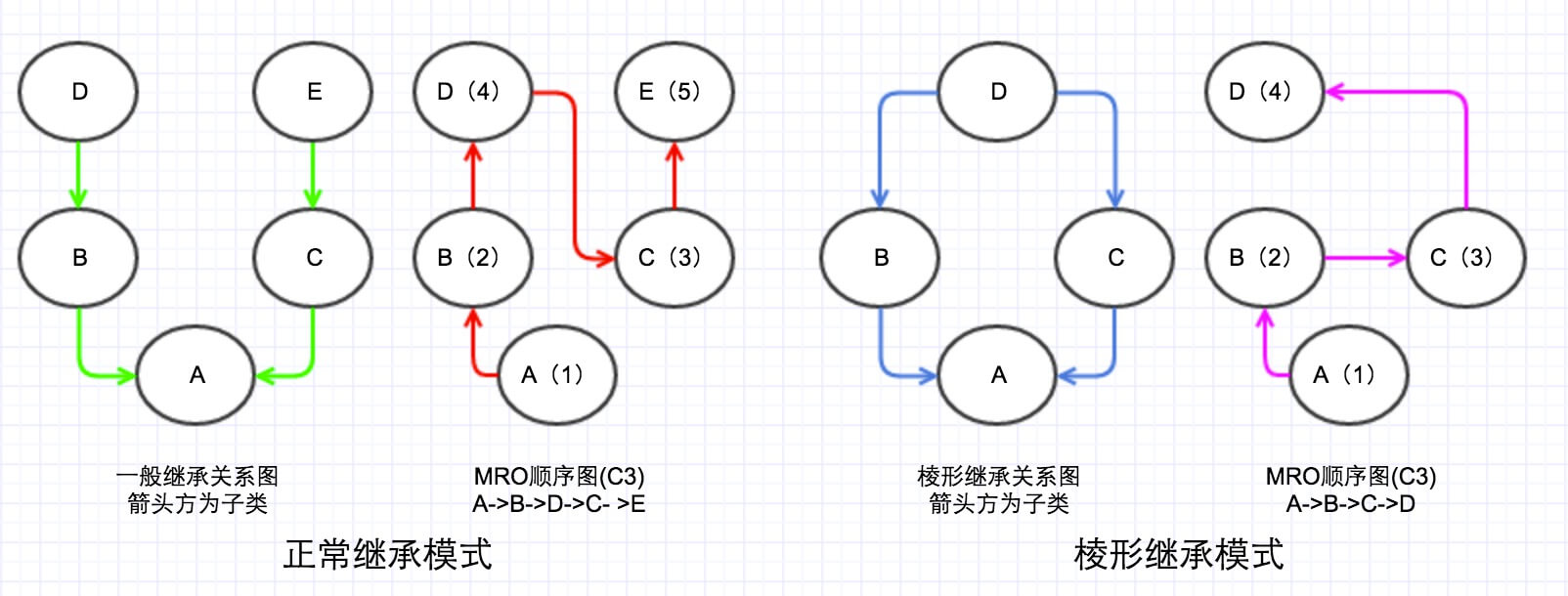
左边类 DFS，右边类 BFS

Python3 到至今：新式类一统江湖

Python3 开始就只存在新式类了，采用的 MRO 也依旧是 C3 算法。

C3 算法解决了单调性问题和只能继承无法重写问题，在很多技术文章包括官网中的 C3 算法，都只有那个 merge list 的公式法，想看的话网上很多，自己可以查。但是从公式很难理解到解决这个问题的本质。我经过一番思考后，我讲讲我所理解的 C3 算法的本质。如果错了，希望有人指出来。假设继承关系如下(官网的例子)：

class D(object):
    pass

class E(object):
    pass

class F(object):
    pass

class C(D, F):
    pass

class B(E, D):
    pass

class A(B, C):
    pass

if __name__ == '__main__':
    print A.__mro__

首先假设继承关系是一张图（事实上也是），我们按类继承是的顺序（class A(B, C)括号里面的顺序B, C），子类指向父类，构一张图。

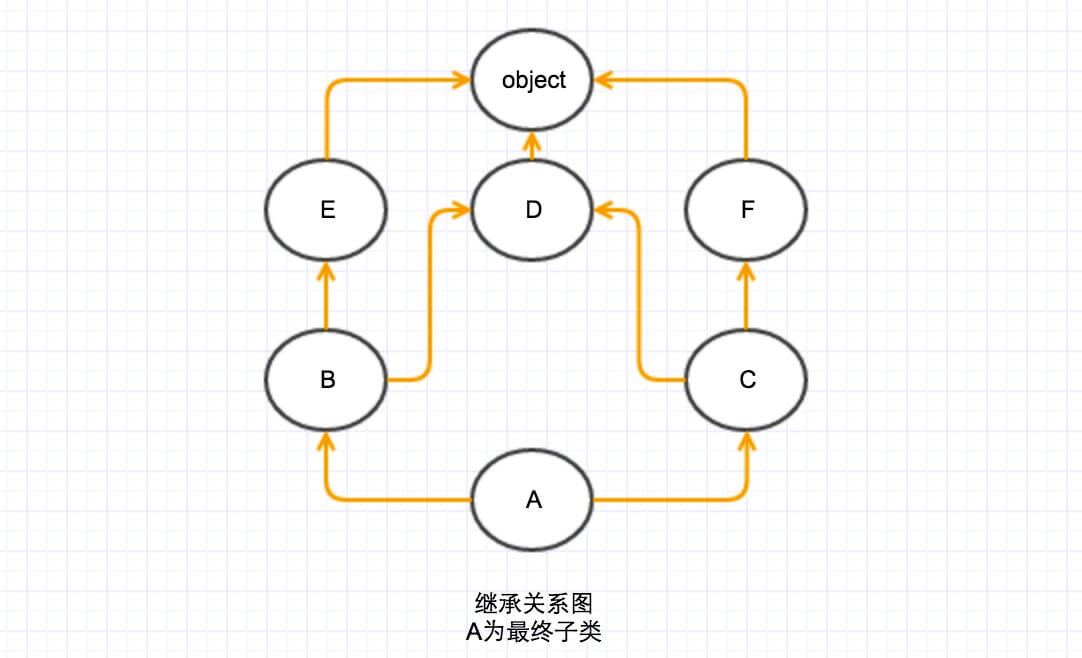
我们要解决两个问题：单调性问题和不能重写的问题。

很容易发现要解决单调性，只要保证从根(A)到叶(object)，从左到右的访问顺序即可。

那么对于只能继承，不能重写的问题呢？先分析这个问题的本质原因，主要是因为先访问了子类的父类导致的。那么怎么解决只能先访问子类再访问父类的问题呢？如果熟悉图论的人应该能马上想到拓扑排序，这里引用一下百科的的定义:

对一个有向无环图(Directed Acyclic Graph, 简称 DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

因为拓扑排序肯定是根到叶（也不能说是叶了，因为已经不是树了），所以只要满足从左到右，得到的拓扑排序就是结果，关于拓扑排序算法，大学的数据结构有教，这里不做讲解，不懂的可以自行谷歌或者翻一下书，建议了解完算法再往下看。

那么模拟一下例子的拓扑排序：首先找入度为 0 的点，只有一个A，把A拿出来，把A相关的边剪掉，再找下一个入度为0的点，有两个点(B,C)，取最左原则，拿B，这是排序是AB，然后剪B相关的边，这时候入度为0的点有E和C，取最左。这时候排序为ABE，接着剪E相关的边，这时只有一个点入度为0，那就是C，取C，顺序为ABEC。剪C的边得到两个入度为0的点（DF），取最左D，顺序为ABECD，然后剪D相关的边，那么下一个入度为0的就是F，然后是object。那么最后的排序就为ABECDFobject。

不理解：这个过程的算法由什么语言完成呢？

对比一下 A.__mro__的结果

(<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <type 'object'>)

完全正确！本应该就这里完了，但是后期一些细心的读者还是发现了问题。以上算法并不完全正确。感谢@Tiger要好好写论文指出。

下面我们来看看这个问题：Tiger 指出了两点，一点是图中左右顺序比较难区分，还有一点是某种不可序列化的情况下，我的算法会有一些问题，针对这两点我做了改进。

先来看看出错的情况：

class A(object):
    pass

class B(object):
    pass

class C(A, B):
    pass

class D(B, A):
    pass

class E(C, D):
    pass

构成对应的图，如下其中橙色的线是改进的地方。

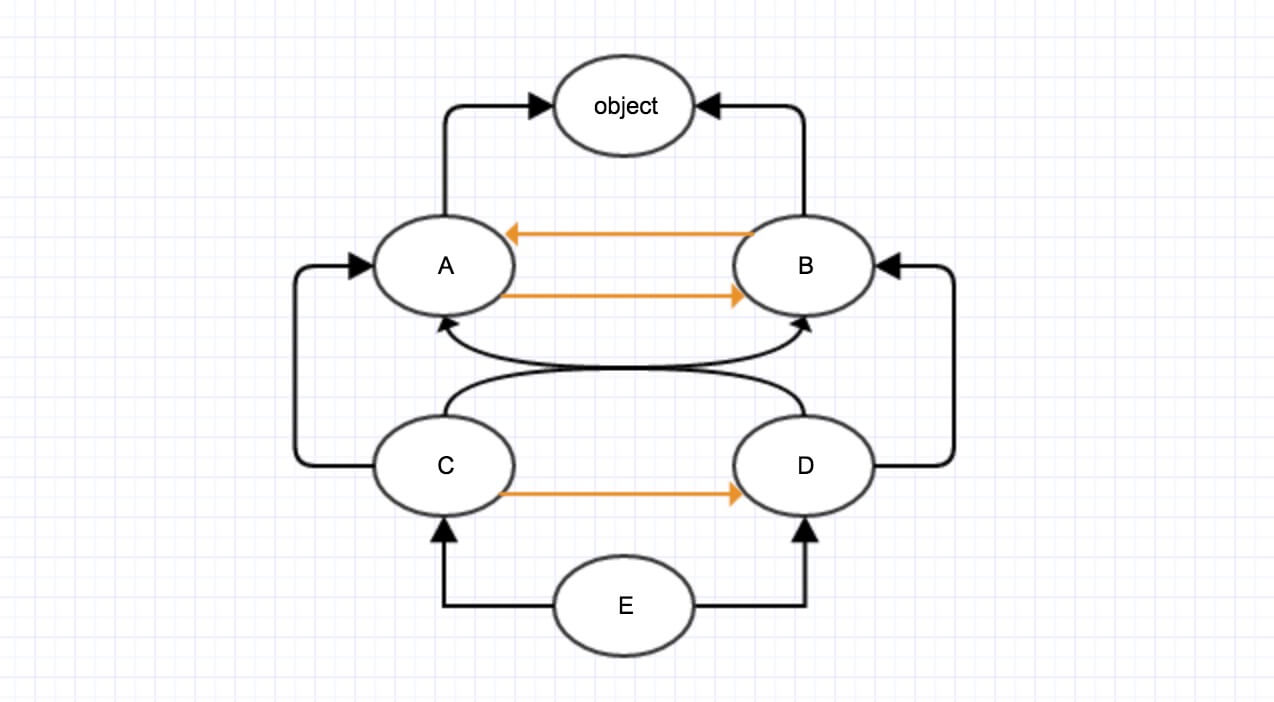
如果使用原来的算法，我们搞不清楚A和B谁在左边谁在右边，所以会选择其中之一，继续拓扑下去，其实这里已经是有歧义了不能够解析出正确的顺序，应该报错，这使我重新思考了左右的问题。

我们可以发现其中左右问题无非出现在两种情况，第一种情况是：图中E先继承C，再继承D；第二种情况是：先继承C的基类，再去继承D。针对这两种情况给出的方案就是图中添加的橙色的边，表示的是第一种情况的顺序问题，比如C->D，就是表示E(C,D>中的继承顺序。

那么第二种情况怎么保证先C的基类，然后再考虑D呢。我们可以这么做，如果出现多个入度为 0 的点，我们先找是刚刚剪出来的点的基类的点。这里可以看之前官网的那个例子，在E点和C点选择的时候，因为E是B的基类点，所以先选它，其实这也很容易实现，只需要记录下每个节点的子类点（可能有多个）。

那么左右的问题也就解决了。

你真的理解 Python 中的 MRO 算法吗？z

前言